1、若双曲线\(M\)上存在四个点\(A\)、\(B\)、\(C\)、\(D\),使得四边形\(ABCD\)是正方形,则双曲线\(M\)的离心率的取值范围是________.
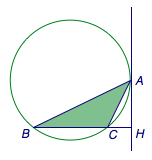
2、以\(C\)为钝角的三角形\(ABC\)中,\(BC=3\),\(\overrightarrow{BA}\cdot\overrightarrow{BC}=12\),当角\(A\)最大时,三角形\(ABC\)的面积为_______.
3、设函数\(f(x)\)在\(\mathcal R\)上存在导函数\(f'(x)\).对任意实数\(x\),均有\(f(-x)+f(x)=x^2\),且当\(x\in (0,+\infty)\),\(f'(x)>x\).若有\(f(1-a)-f(a)\geqslant \dfrac 12-a\),则实数\(a\)的取值范围是________.
4、若\(a>1\),函数\(f(x)=a^x-x^2\)有三个不同的零点,则实数\(a\)的取值范围是_______.
5、已知函数\(f(x)=\left|x^3-4x\right|+ax-2\)恰有\(2\)个零点,则实数\(a\)的取值范围为_______.
6、已知\(\forall x\in (0,1),{\mathrm e}^x+ax-1\geqslant x^2\),则\(a\)的取值范围是_______.
7、求证:函数\(f(x)={\mathrm e}^x-ax+a\)的两个零点\(x_1\)、\(x_2\)满足\(x_1x_2<x_1+x_2\).
参考答案
1、\(\left(\sqrt 2,+\infty\right)\)
2、\(3\).
提示:利用平面向量数量积的几何意义、“等张角线”、切割线定理,如图.
3、\(\left(-\infty,\dfrac 12\right]\)
提示:构造函数\(g(x)=f(x)-\dfrac 12x^2\),则函数\(g(x)\)是\(\mathcal R\)上单调递增的奇函数,且\(g(1-a)\geqslant g(a)\).
4、\(\left(1,{\mathrm e}^{\frac{2}{\mathrm e}}\right)\).
提示:可以分离变量转化为\(\ln a=\dfrac{2\ln x}{x}\)在\(x>0\)时有两个解.
5、\(\left(-\infty,-1\right)\cup\left(1,+\infty\right)\)
6、\(\left[2-\mathrm e,\infty\right)\)
7、提示:即证明\(g(x)={\mathrm e}^{x+1}-ax\)的两个零点\(x_1\)、\(x_2\)满足\(x_1x_2<1\).接下来利用齐次换元就可以证明.