每日一题[1133]双变元最值问题

已知变量 $x$ 和 $\theta$ 都在 $\mathbb R$ 上变化，则 $\dfrac{x^2+2x\sin\theta+2}{x^2+2x\cos\theta+2}$ 的取值范围是_______．

---

正确答案是$\left[2-\sqrt 3,2+\sqrt 3\right]$．

分析与解　法一　根据题意，有

$$\dfrac{x^2+2x\sin\theta+2}{x^2+2x\cos\theta+2}=\begin{cases} 1,&x=0,\\ \dfrac{u+\sin\theta}{u+\cos\theta},&x\ne 0,\end{cases}$$ 其中 $u=\dfrac x2+\dfrac 1x$，$u$ 的取值范围是 $\left(-\infty,-\sqrt 2\right]\cup\left[\sqrt 2,+\infty\right)$．考虑几何意义和图形的对称性，有 $$k=\dfrac{u+\sin\theta}{u+\cos\theta}$$ 的取值范围是射线 $y=x$，$x\in\left[\sqrt 2,+\infty\right)$ 上的点到单位圆上的点的斜率的取值范围，为 $\left[2-\sqrt 3,2+\sqrt 3\right]$．

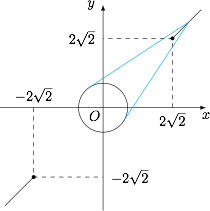
综上所述，所求的取值范围是 $\left[2-\sqrt 3,2+\sqrt 3\right]$．

法二　设题中代数式为 $t$，则

$$(1-t)x^2+\left(2\sin\theta-2\cos\theta\cdot t\right)x+2-2t=0,$$ 其判别式 $$\Delta=4\left(\sin\theta-\cos\theta\cdot t\right)^2-8(1-t)^2\geqslant 0,$$ 于是 $$|\sin\theta-t\cos\theta|\geqslant \sqrt 2|1-t|,$$ 于是 $$\sqrt{1+t^2}\geqslant \sqrt 2|1-t|,$$ 解得 $t$ 的取值范围是 $\left[2-\sqrt 3,2+\sqrt 3\right]$．