已知函数 \(f(x)=\left|x+\dfrac 1x\right|+\left|m-x+\dfrac{1}{m-x}\right|-a\) 有 \(6\) 个零点，且所有零点之和为 \(3\)，则 \(a\) 的取值范围是_______．
正确答案是\((5,+\infty)\)．
分析与解 根据题意，有\[f(x)=f(m-x),\]于是函数 \(f(x)\) 关于 \(x=\dfrac 12m\) 对称．结合所有的零点的平均数为 \(\dfrac 12\)，可得 \(m=1\)．此时问题转化为函数\[g(x)=\left|x+\dfrac 1x\right|+\left|1-x+\dfrac{1}{1-x}\right|\]在 \(\left(\dfrac 12,+\infty\right)\) 上与直线 \(y=a\) 有 \(3\) 个公共点．此时\[g(x)=\begin{cases} \dfrac 1x+\dfrac{1}{1-x}+1,&\dfrac 12<x<1,\\2x+\dfrac 1x+\dfrac{1}{x-1}-1,&x>1.\end{cases}\]
情形一 当 \(\dfrac 12<x<1\) 时，函数 \(g(x)\) 的导函数\[g'(x)=-\dfrac 1{x^2}+\dfrac{1}{(1-x)^2}>0,\]于是函数 \(g(x)\) 单调递增，且取值范围是 \((5,+\infty)\)．（也可以不求导，由\[ g(x)=1+\dfrac 1{x(1-x)} \]知 \( g(x)\) 在 \( \left(\dfrac 12,1\right)\) 上单调递增．）
情形二 当 \( x>1 \) 时，函数 \( g(x)\) 的导函数\[g'(x)=2-\dfrac{1}{x^2}-\dfrac{1}{(x-1)^2},\]考虑到 \( g'(x)\) 是 \((1,+\infty)\) 上的单调递增函数，且\[\lim_{x\to 1^+}g'(x)=-\infty,\lim_{x\to +\infty}g'(x)=2,\]于是 \( g'(x)\) 在 \((1,+\infty)\) 上有唯一零点，记为 \( x_0 \)．进而函数 \( g(x)\) 在 \((1,x_0)\) 上单调递减，在 \((x_0,+\infty)\) 上单调递增，在 \( x=x_0 \) 处取得极小值 \( m \)，如图．
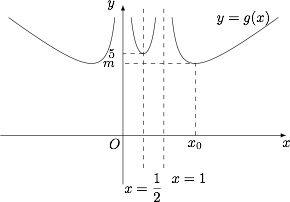接下来问题的关键是判断 \( m \) 与 \( 5 \) 的大小关系．注意到\[m\leqslant f\left(\dfrac 32\right)=\dfrac 32+\dfrac 23+\dfrac 12+2=\dfrac{14}{3}<5,\]于是所求的取值范围是 \((5,+\infty)\)．
注 事实上，极小值点\[x_0=\dfrac{1+\sqrt{3+2\sqrt 3}}2\approx 1.7712,\]对应的极小值\[m=\sqrt{9+6\sqrt 3}\approx 4.4037.\]