每日一题[1066]适当放缩

求证：${\rm e}^x+\left(\ln x-1\right)\cdot \sin x>0$．

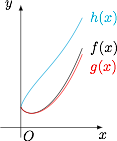
分析与证明　记不等式左边为 $f(x)$．考虑到当 $x>0$ 时，有 $-x<\sin x<x$，于是设 $$\begin{split}g(x)&={\rm e}^x+\left(\ln x-1\right)\cdot x,\\h(x)&={\rm e}^x+\left(\ln x-1\right)\cdot (-x),\end{split}$$ 则 $f(x)$ 必然在 $g(x)$ 和 $h(x)$ 之间，如图．

接下来证明 $g(x)>0$ 且 $h(x)>0$．

一方面，有 $$g(x)={\rm e}^x-x +x\ln x,$$ 而 $\left({\rm e}^x-x\right)'={\rm e}^x-1$，于是 $${\rm e}^x-x\geqslant {\rm e}^0-0=1.$$ 由 $\left(x\ln x\right)'=1+\ln x$，于是 $$x\ln x\geqslant -\dfrac{1}{\rm e},$$ 考虑到两个等号无法同时取得，因此有 $$g(x)> 1-\dfrac{1}{\rm e}.$$

另一方面，由 $1-\ln x\geqslant 2-x$，于是有 $$h(x)\geqslant {\rm e}^x+(2-x)x,$$ 而 $$\left({\rm e}^x+(2-x)x\right)'={\rm e}^x-2x+2>0,$$ 于是 $y={\rm e}^x+(2-x)x$ 单调递增，进而有 $h(x)>1$．

综上所述，原命题得证．

注　事实上，我们证明了一个更强的命题： $${\rm e}^x+\left(\ln x-1\right)\cdot \sin x>1-\dfrac{1}{\rm e}.$$