函数$f(x)=\dfrac{4x}{x+1}$($x>0$)，$g(x)=\dfrac 12\left(|x-a|-|x-b|\right)$($a<b$)，若对$\forall x_1>0$，$\exists x_2\leqslant x_1$，$g(x_2)=f(x_1)$，则$2a+b$的最大值为________．
正确答案是$-7$．
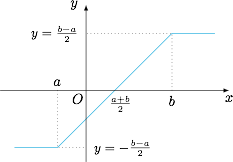
分析与解 函数$g(x)$的图象是反Z字型，对称中心为$P\left(\dfrac{b+a}2,0\right)$，斜线部分斜率为$1$，水平部分的函数值分别为$-\dfrac{b-a}2$和$\dfrac{b-a}2$，如图．
取函数$f(x)$斜率为$1$的切线$y=x+1$，如图：
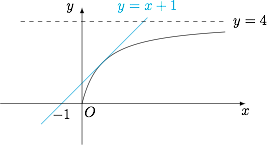根据题意，有\[\begin{cases}\dfrac{b+a}2\leqslant -1,\\ \dfrac{b-a}2\geqslant 4,\end{cases}\]因此\[2a+b=\dfrac 32(b+a)-\dfrac 12(b-a)\leqslant -7,\]当$(a,b)=(-5,3)$时取得等号．因此所求的最大值为$-7$．
注 本题为尬题16．