已知三条平行直线$a,b,c$($b$在$a,c$之间),点$A$在直线$a$上,求作正$\triangle ABC$,使顶点$B$在直线$b$上,顶点$C$在直线$c$上.
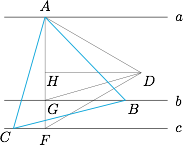 作法
作法
(1) 作$AF\perp c$且分别交直线$b,c$于点$G,F$;
(2) 以$AF$为底边作正三角形$ADF$;
(3) 过$D$作$AF$的垂线,垂足为$H$;
(4) 将射线$AD$按$\angle GDH$旋转交直线$b$于点$B$;
(5) 以$AB$为底边作正三角形$ABC$.
证明 由于$\triangle ADF$与$\triangle ABC$均为正三角形,因此$\triangle ADB$与$\triangle AFC$旋转全等.考虑到\[\angle BAD=\angle GDH=\angle BGD,\]于是$A,G,B,D$四点共圆,进而可得$\angle ADB+\angle AGB=180^\circ$,于是$\angle ADB=90^\circ$,于是$$\angle AFC=\angle ADB=90^\circ,$$于是$C\in c$,这就证明了作法的正确性.

