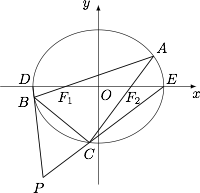
已知椭圆$E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的内接$\triangle ABC$的边$AB,AC$分别过其左、右焦点$F_1(-c,0),F_2(c,0)$,椭圆$E$的左、右顶点分别为$D,E$,直线$DB$和$EC$交于点$P$,当点$A$在椭圆$E$上运动时,点$P$的轨迹方程是__________.
正确答案是\[\dfrac{x^2}{a^2}+\dfrac{y^2}{\left(b\cdot \dfrac{c+a}{c-a}\right)^2}=1,y\ne 0.\]
分析与解 设$A(a\cos 2\alpha,b\sin 2\alpha)$,$B(a\cos2\beta,b\sin2\beta)$,$C(a\cos2\gamma,b\sin2\gamma)$,则由椭圆的参数弦方程可得直线$AB$的横截距$-c$满足\[\tan\alpha\cdot \tan\beta=\dfrac{-c-a}{-c+a},\]直线$AC$的横截距$c$满足\[\tan\alpha\cdot \tan\gamma =\dfrac{c-a}{c+a},\]因此直线$BD$和直线$EC$的斜率$k_{PD},k_{PE}$的乘积为\[\begin{split}k_{PD}\cdot k_{PE}&=\dfrac{b\sin2\beta}{a\cos2\beta+a}\cdot \dfrac{b\sin2\gamma}{a\cos{2\gamma} -a}\\
&=\dfrac{b^2}{a^2}\cdot \tan\beta \cdot \left(-\dfrac{1}{\tan\gamma}\right)\\
&=-\dfrac{b^2}{a^2}\cdot \left(\dfrac{c+a}{c-a}\right)^2.
\end{split}\]根据椭圆的斜率积定义,可得点$P$的轨迹方程是\[\dfrac{x^2}{a^2}+\dfrac{y^2}{\left(b\cdot \dfrac{c+a}{c-a}\right)^2}=1,y\ne 0.\]