解方程\(x^3-3x=\sqrt{x+2}\)．
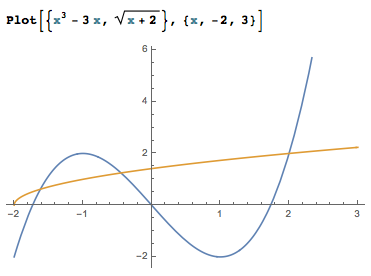注意到\[4\cdot\left(\dfrac x2\right)^3-3\cdot\dfrac{x}{2}=\sqrt{\dfrac{\dfrac x2+1}{2}},\]联想余弦的三倍角和半角公式，令\(\dfrac x2=\cos \theta\)，\(\theta\in [0,\pi]\)，则\[4\cos^3\theta-3\cos\theta=\sqrt{\dfrac{1+\cos\theta}{2}},\]即\[\cos{3\theta}=\cos\dfrac{\theta}{2},\]解得\[3\theta=\dfrac{\theta}{2}\lor 3\theta=2\pi -\dfrac{\theta}{2}\lor 3\theta=2\pi+\dfrac{\theta}{2},\]即\[\theta=0,\dfrac{4\pi}{7},\dfrac{4\pi}5,\]于是\[x=2,2\cos\dfrac{4\pi}7,2\cos\dfrac{4\pi}5.\]