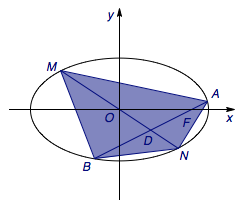
（2015年北京市朝阳区高三一模理科数学）已知椭圆\(C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)（\(a>b>0\)）的一个焦点为\(F(2,0)\)，离心率为\(\dfrac{\sqrt 6}{3}\)．过焦点\(F\)的直线\(l\)与椭圆\(C\)交于\(A\)、\(B\)两点，线段\(AB\)的中点为\(D\)，\(O\)为坐标原点，过\(O\)、\(D\)的直线交椭圆于\(M\)、\(N\)两点．
（1）求椭圆\(C\)的方程；
（2）求四边形\(AMBN\)面积的最大值．
（1）容易求得椭圆\(C:\dfrac{x^2}{6}+\dfrac{y^2}{2}=1\)；
（2）根据题意可得\[AMBN=\dfrac 12\cdot AB\cdot MN \cdot \sin\langle AB,MN\rangle,\]其中\(AB\)、\(MN\)及\(\langle AB,MN\rangle\)均随着直线\(l\)的运动而改变．
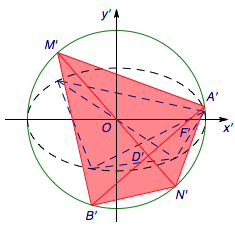
考虑用伸缩变换将其拉成圆，只需要将每个点的纵坐标变成原来的\(\sqrt 3\)倍，横坐标不变即可，如图．
此时\(M'N'\)为圆\(x'^2+y'^2=6\)的直径为定值\(2\sqrt 6\)，而由垂径定理\(\langle A'B',M'N'\rangle=\dfrac{\pi}{2}\)亦为定值，此时可得\[A'M'B'N'=\sqrt 6A'B'\leqslant \sqrt 6\cdot 2\sqrt 6=12,\]等号当且仅当\(A'B'\)为直径，也即直线\(l:y=0\)时取得，此时四边形\(AMBN\)的面积取得最大值\[\dfrac{A'M'B'N'}{\sqrt 3}=4\sqrt 3.\]