每日一题[941]曲线间距离

设$P$为曲线$C_1$上的动点，$Q$为曲线$C_2$上的动点，则称$|PQ|$的最小值为曲线 $C_1,C_2$之间的距离，记作$d\left(C_1,C_2\right)$．
(1)若

$$C_1:x^2+y^2=2,\ C_2:(x-3)^2+(y-3)^2=2,$$ 则$d\left(C_1,C_2\right)=$_______；
(2)若 $$C_3:\mathrm{e}^x-2y=0,\ C_4:\ln x+\ln 2=y,$$ 则$d\left(C_3,C_4\right)=$_______．

---

正确答案是$\sqrt{2}$；$\sqrt{2}-\sqrt{2}\ln 2$．

分析与解　(2)注意$C_3$与$C_4$的图象关于直线$y=x$对称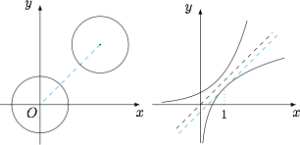．所以只需要求曲线$C_4$上的点到$y=x$的距离的最小值，$C_4$对应的函数为$y=\ln x+\ln 2$，所以斜率为$1$的切线方程对应的切点为$(1,\ln 2)$，从而切线为$y=x-1+\ln 2$，它与$y=x$的距离为

$$d=\dfrac{1-\ln 2}{\sqrt 2},$$ 从而 $$d(C_3,C_4)=2\cdot\dfrac{1-\ln 2}{\sqrt 2}=\sqrt 2-\sqrt 2\ln 2.$$