每日一题[874]椭圆的光学性质

对于两条垂直直线和一个椭圆，已知椭圆无论如何滑动都与两条直线相切，求椭圆中心的轨迹．

---

分析与解　由椭圆的几何性质，

$$\left| {{F_1}^\prime {F_2}} \right| = \left| {{F_1}{F_2}^\prime } \right| = 2a.$$
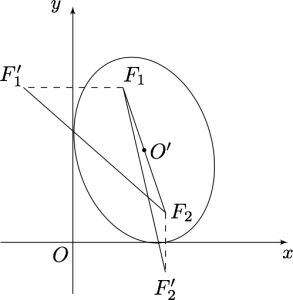而设$O'\left( {x,y} \right)$，则${F_1}\left( {x - c\cos \theta ,y + c\sin \theta } \right)$，${F_2}\left( {x + c\cos \theta ,y - c\sin \theta } \right)$，

${F_1}^\prime \left( { - x + c\cos \theta ,y + c\sin \theta } \right)$，${F_2}^\prime \left( {x + c\cos \theta , - y + c\sin \theta } \right)$．

所以

$${\left| {{F_1}{F_2}^\prime } \right|^2} = 4{a^2} = 4{c^2}{\cos ^2}\theta + 4{y^2},$$ $${\left| {{F_2}{F_1}^\prime } \right|^2} = 4{a^2} = 4{c^2}{\sin ^2}\theta + 4{x^2}.$$ 两式相加，有 $${x^2} + {y^2} = 2{a^2} - {c^2} = {a^2} + {b^2}.$$
所以$P$点的轨迹是以两条垂直的直线交点为圆心，$\sqrt {{a^2} + {b^2}}$为半径的圆．