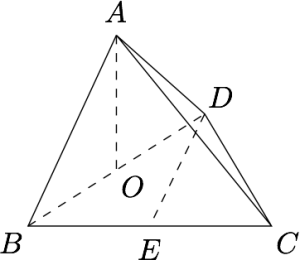
如图,四面体$ABCD$中,$O,E$分别是$BD,BC$的中点,$AO$垂直于平面$BCD$,且$CA = CB = CD = 2$,$AB = \sqrt 2 $,求异面直线$AB$与$ED$所成角的大小.
分析与解 记$$\overrightarrow {CA} = 2\overrightarrow a\;,\;\overrightarrow {CB} = 2\overrightarrow b\;,\;\overrightarrow {CD} = 2\overrightarrow c ,$$其中$\overrightarrow a ,\overrightarrow b,\overrightarrow c $均为单位向量,则$$\overrightarrow{CO}=\overrightarrow b + \overrightarrow c\;,\;\overrightarrow{CE}=\overrightarrow b\;,\;\overrightarrow {AO} = \overrightarrow b + \overrightarrow c - 2\overrightarrow a ,$$而$AO$垂直于平面$BCD$,于是$$\left( {\overrightarrow b + \overrightarrow c - 2\overrightarrow a } \right) \cdot \overrightarrow b = \left( {\overrightarrow b + \overrightarrow c - 2\overrightarrow a } \right) \cdot \overrightarrow c = 0,$$即$$\overrightarrow b \cdot \overrightarrow c - 2\overrightarrow a \cdot \overrightarrow b + 1 = 0\;,\;\overrightarrow b \cdot \overrightarrow c - 2\overrightarrow a \cdot \overrightarrow c + 1 =0\qquad\cdots\cdots(i),$$ 又$AB = \sqrt 2 $,于是$\left( {2\overrightarrow a - 2\overrightarrow b } \right) \cdot \left( {2\overrightarrow a - 2\overrightarrow b } \right) = 2$,即$$\overrightarrow a \cdot \overrightarrow b = \dfrac{3}{4}\qquad\cdots\cdots(ii),$$由$(i)(ii)$,得$$\overrightarrow b \cdot \overrightarrow c = \dfrac{1}{2}\;,\;\overrightarrow a \cdot \overrightarrow c = \dfrac{3}{4},$$又 $\overrightarrow {AB} = 2\overrightarrow b - 2\overrightarrow a $,$\overrightarrow {ED} = 2\overrightarrow c - \overrightarrow b $,于是异面直线$AB$与$ED$所成角$\theta $满足$$\cos \theta = \dfrac{{\left| {\left( {2\overrightarrow b - 2\overrightarrow a } \right)\cdot\left( {2\overrightarrow c - \overrightarrow b } \right)} \right|}}{{\sqrt 2 \cdot \sqrt {\left( {2\overrightarrow c - \overrightarrow b } \right)\cdot\left( {2\overrightarrow c - \overrightarrow b } \right)} }} = \dfrac{|{4\overrightarrow b \cdot \overrightarrow c - 2 - 4\overrightarrow a \cdot \overrightarrow c + 2\overrightarrow a \cdot \overrightarrow b }|}{{\sqrt 2 \cdot \sqrt { {4 - 4\overrightarrow b \cdot \overrightarrow c + 1} } }} = \dfrac{{\sqrt 6 }}{4},$$因此,所求角为$\arccos \dfrac{{\sqrt 6 }}{4}$.