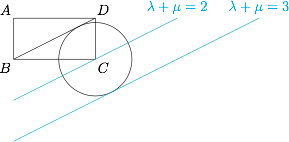(理12)在矩形$ABCD$中，$AB=1$，$AD=2$，动点$P$在以点$C$为圆心且与$BD$相切的圆上，若$\overrightarrow{AP}=\lambda \overrightarrow{AB}+\mu \overrightarrow{AD}$，则$\lambda+\mu$的最大值为( )
A．$3$
B．$2\sqrt 2$
C．$\sqrt 5$
D．$2$
分析与解 A．
如图，考虑向量线性分解的等系数和线，可得$\lambda+\mu$的最大值为$3$．
(理16)$a,b$为空间中两条互相垂直的直线，等腰直角三角形$ABC$的直角边$AC$所在直线与$a,b$都垂直，斜边$AB$以直线$AC$为旋转轴旋转，有下列结论；
(1) 当直线$AB$与$a$成$60^\circ$角时，$AB$与$b$成$30^\circ$角；
(2) 当直线$AB$与$a$成$60^\circ$角时，$AB$与$b$成$60^\circ$角；
(3) 直线$AB$与$a$所成角的最小值为$45^\circ$；
(4) 直线$AB$与$a$所成角的最大值为$90^\circ$．
其中正确的是________．
分析与解 (2)(3)．
如图，设$CD$为直线$a$，$CE$为直线$b$，过$B$分别作$a,b$的平行线$BM,BN$，设$\angle CBM=\theta$，直线$AB$与直线$a,b$所成的角分别为$\alpha,\beta$．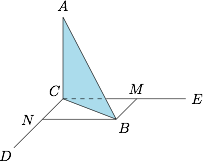
根据三射线定理，有\[\cos\alpha=\cos\angle ABM=\cos\angle CBA\cdot \cos\angle CBM=\dfrac{\sqrt 2}2\cdot \cos\theta,\]类似的，有\[\cos\beta=\cos\angle ABN=\cos\angle CBA\cdot \cos \angle CBN=\dfrac{\sqrt 2}2\cdot\sin\theta,\]据此易得命题(2)(3)正确．
注 直线$AB$与直线$a,b$所成的角分别为$\alpha,\beta$，三射线定理部分也可以通过建系解决，令$\overrightarrow{a}=(1,0,0),\overrightarrow{b}=(0,1,0)$，则可以取$C(0,0,0),A(0,0,1)$，则点$B$可以设为$(\cos\theta,\sin\theta,0)$，于是$\overrightarrow{AB}=(\cos\theta,\sin\theta,-1)$，从而有$$\overrightarrow{AB}\cdot\overrightarrow{a}=\cos \theta=\sqrt 2\cos\alpha,\overrightarrow{AB}\cdot\overrightarrow{b}=\sin\theta=\sqrt 2\cos\beta.$$以下同上．
(理20)已知抛物线$C:y^2=2x$，过点$(2,0)$的直线$l$交$C$于$A,B$两点，圆$M$是以线段$AB$为直径的圆．
(1) 证明：坐标原点$O$在圆$M$上；
(2) 设圆$M$过点$P(4,-2)$，求直线$l$与圆$M$的方程．
分析与解 (1) 设$A(2a^2,2a)$，$B(2b^2,2b)$，则\[\dfrac{2a^2\cdot 2b-2b^2\cdot 2a}{2b-2a}=-2ab=2,\]即$ab=-1$，因此\[\overrightarrow{OA}\cdot \overrightarrow{OB}=2a^2\cdot 2b^2+2a\cdot 2b=4ab(ab+1)=0,\]因此命题得证．
(2) 根据题意，有\[\begin{split}\overrightarrow{PA}\cdot \overrightarrow{PB}&=(2a^2-4)(2b^2-4)+(2+2a)(2+2b)\\&=4a^2b^2-8(a^2+b^2)+4ab+4(a+b)+20\\&=-8\left[(a+b)^2-2ab\right]+4(a+b)+20\\&=-8(a+b)^2+4(a+b)+4\\&=0,\end{split}\]解得$a+b=1$或$a+b=-\dfrac 12$．而直线$l$的方程为\[x=\dfrac{2a^2-2b^2}{2a-2b}y+2,\]即\[x=(a+b)y+2,\]圆$M$的圆心坐标为$\left(a^2+b^2,a+b\right)$，因此当$a+b=1$时，直线$l$的方程为$y=x-2$，圆$M$的圆心坐标为$(3,1)$，圆$M$的方程为\[(x-3)^2+(y-1)^2=10.\]当$a+b=-\dfrac 12$时，直线$l$的方程为$y=-2x+4$，圆$M$的圆心坐标为$\left(\dfrac 94,-\dfrac 12\right)$，圆$M$的方程为\[\left(x-\dfrac 94\right)^2+\left(y+\dfrac 12\right)^2=\dfrac{85}{16}.\]
(理21)已知函数$f(x)=x-1-a\ln x$．
(1) 若$f(x)\geqslant 0$，求$a$的值；
(2) 设$m$为整数，且对于任意正整数$n$，有\[\left(1+\dfrac 12\right)\left(1+\dfrac{1}{2^2}\right)\cdots\left(1+\dfrac{1}{2^n}\right)<m,\]求$m$的最小值．
分析与解 (1) 当$a\leqslant 0$时，有$$f\left({\rm e}^{-1}\right)={\rm e}^{-1}-1+a<0,$$不符合题意；
当$0<a<1$时，函数$f(x)$的导函数$$f'(x)=\dfrac{x-a}{x},$$于是在区间$(a,1)$上，函数$f(x)$单调递增，而$f(1)=0$，因此在该区间上$f(x)<0$，不符合题意；
当$a=1$时，容易证明$x-1-\ln x\geqslant 0$，符合题意；
当$a>1$时，在区间$(1,a)$上，函数$f(x)$单调递减，而$f(1)=0$，因此在该区间上$f(x)<0$，不符合题意．
综上所述，$a$的值为$1$．
(2) 一方面，当$n=3$时，有$$LHS=\dfrac 32\cdot \dfrac 54\cdot \dfrac 98=\dfrac{135}{64},$$于是$m\geqslant 3$．
另一方面，有\[\begin{split}&\ln \left[\left(1+\dfrac 12\right)\left(1+\dfrac{1}{2^2}\right)\cdots\left(1+\dfrac{1}{2^n}\right)\right]\\=&\ln \left(1+\dfrac 12\right)+\ln\left(1+\dfrac 1{2^2}\right)+\cdots+\ln\left(1+\dfrac{1}{2^n}\right)\\<&\dfrac 12+\dfrac{1}{2^2}+\cdots+\dfrac{1}{2^n}\\=&1-\dfrac{1}{2^n}<1,\end{split}\]因此有\[\left(1+\dfrac 12\right)\left(1+\dfrac{1}{2^2}\right)\cdots\left(1+\dfrac{1}{2^n}\right)<{\rm e},\]因此$m$可以取到$3$．
综上所述，$m$的最小值为$3$．