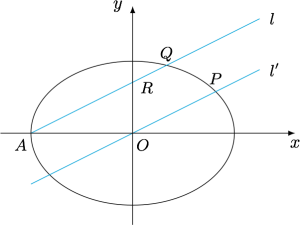
已知椭圆$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$,过椭圆左顶点$A\left( -a,0 \right)$的直线$l$与椭圆交于$Q$,与$y$轴交于$R$,过原点与$l$平行的直线与椭圆交于$P$.求证:$AQ$,$\sqrt{2}OP$,$AR$成等比数列.

分析与解 如图,设过原点与$l$平行的直线为${l}'$,$l$的斜率为$k$,
则取$\left( 1,k \right)$为直线$l$与${l}'$共同的方向向量,则直线$l$与$l'$的参数方程为$$\begin{cases}x=-a+t \\ y=kt \end{cases}\ \text{与}\ \begin{cases}x=t \\ y=kt \end{cases}$$
欲证结论为${{\left( \sqrt{2}{{t}_{p}} \right)}^{2}}={{t}_{Q}}\cdot {{t}_{R}}$,即$$2{{t}_{P}}^{2}={{t}_{R}}{{t}_{Q}},$$因为$R$的横坐标为$0$,于是${{t}_{R}}=a$;
联立直线$l$的参数方程与椭圆方程,有$$\dfrac{{{\left( t-a \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}{{t}^{2}}}{{{b}^{2}}}=1,$$解得${{t}_{Q}}=\dfrac{2}{\frac{1}{{{a}^{2}}}+\frac{{{k}^{2}}}{{{b}^{2}}}}\cdot \dfrac{1}{a}$;
联立直线${l}'$的参数方程与椭圆方程,有$\dfrac{{{t}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}{{t}^{2}}}{{{b}^{2}}}=1$,于是$${{t}_{P}}^{2}=\dfrac{1}{\frac{1}{{{a}^{2}}}+\frac{{{k}^{2}}}{{{b}^{2}}}}.$$
显然,$2{{t}_{p}}^{2}={{t}_{Q}}\cdot {{t}_{R}}$成立,于是命题得证.