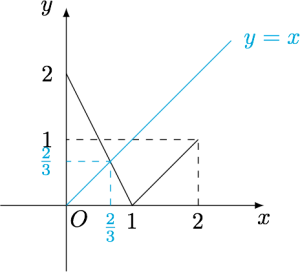
已知函数$f(x)=\begin{cases}(2-[x])\cdot |x-1|,& x\in[0,2),\\1,&x=2,\end{cases}$其中$[x]$表示不超过$x$的最大整数.设$n\in\mathbb N^*$,$f_1(x)=f(x)$,$f_{n+1}(x)=f(f_n(x))$,有以下说法:
(1) 函数$y=\sqrt{x-f(x)}$的定义域为$\left[\dfrac 23,2\right]$;
(2) 设集合$A=\{0,1,2\}$,$B=\{x \mid f_3(x)=x,x\in A\}$,则$A=B$;
(3) $f_{2016}\left(\dfrac 89\right)+f_{2017}\left(\dfrac 89\right)=\dfrac{13}9$;
(4) 若集合$M=\{x \mid f_{12}(x)=x,x\in [0,2]\}$,则$M$中至少包含$8$个元素.
指出上述说法中哪些是正确的,并说明理由.
(2) 正确,初值为$0$的迭代序列为$0,2,1,0,2,1,\cdots$.
(3) 错误,考虑到初值为$\dfrac 89$的迭代序列为\[\dfrac 89,\dfrac 29,\dfrac {14}9,\dfrac 59,\dfrac 89,\cdots\]于是所求\[f_{2016}\left(\dfrac 89\right)+f_{2017}\left(\dfrac 89\right)=\dfrac 89+\dfrac 29=\dfrac {10}9\ne \dfrac{13}9.\]
(4) 正确,由(1)(2)(3)可得\[\dfrac 23,0,1,2,\dfrac 89,\dfrac 29,\dfrac{14}9,\dfrac 59\in M.\]
注 事实上,任何分数作为初值的迭代序列都会进入循环,如\[\begin{aligned}\dfrac 13,\dfrac 43,\dfrac 13,\cdots\\\dfrac 15,\dfrac 85,\dfrac 35,\dfrac 45,\dfrac 25,\dfrac 65,\dfrac 15,\cdots \\\dfrac 27,\dfrac {10}7,\dfrac 37,\dfrac 87,\dfrac 17,\dfrac{12}7,\dfrac 57,\dfrac 47,\dfrac 67,\dfrac 27,\cdots\end{aligned}\]