已知椭圆$E:\dfrac{x^2}4+\dfrac{y^2}3=1$,过点$P(2,1)$作直线与椭圆相交于$M,N$,过点$N$作斜率为$-\dfrac 32$的直线与椭圆交于另一点$Q$,求证:直线$MQ$过定点.
分析与解 将椭圆$E$通过仿射变换$x'=x$,$y'=\dfrac{2}{\sqrt 3}y$变成圆$E':x'^2+y'^2=4$,则$P'\left(2,\dfrac{2}{\sqrt 3}\right)$.此时$N'Q'$的斜率为$-\dfrac 32\cdot \dfrac{2}{\sqrt 3}=-\sqrt 3$,因此$Q'$是$N'$关于直线$OP'$的对称点.设直线$OP'$与圆$E'$交于$A',B'$,则直线$M'Q'$与直线$OP'$的交点$R'$满足$R',P'$调和分割$A',B'$.
由于\[|OP'|=\sqrt{2^2+\left(\dfrac{2}{\sqrt 3}\right)^2}=\dfrac{4}{\sqrt 3},\]于是$|OR'|=\sqrt 3$,结合直线$OP'$的倾斜角为$30^\circ$,可得$R'\left(\dfrac 32,\dfrac {\sqrt 3}2\right)$,因此直线$MQ$所过的定点坐标为$\left(\dfrac 32,\dfrac 34\right)$.
注 不利用调和分割性质,直接计算$|OR'|$过程如下:
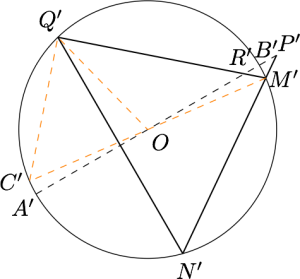
作辅助线如下,则有$$\angle Q'M'O=\dfrac {\pi}2-\angle Q'C'M'=\dfrac {\pi}2-\angle Q'N'P'=\angle A'P'M',$$所以$$\triangle OR'M'\backsim\triangle OM'P',$$从而有$$\dfrac {|OR'|}{|OM'|}=\dfrac {|OM'|}{|OP'|},\Rightarrow |OR'|\cdot |OP'|=|OM'|^2.$$