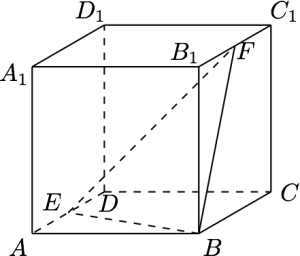
如图，已知正方体$ABCD-A_1B_1C_1D_1$的棱长为$1$，$E,F$分别是棱$AD,B_1C_1$上的动点，设$AE=x$，$B_1F=y$．若棱$DD_1$与平面$BEF$有公共点，则$x+y$的取值范围是________．
正确答案是$[1,2]$．
法一 几何法
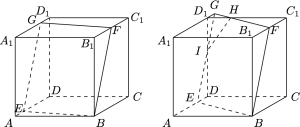
设法作出完整的截面$BEF$，则该截面与上底面$A_1C_1$的交线与直线$BE$平行．过$F$作与$BE$平行的直线$l$，若直线$l$与棱$A_1D_1$相交且交点不为$D_1$，则截面$BEF$为平行四边形，棱$DD_1$与平面$BEF$没有公共点；若直线$l$与棱$A_1D_1$的延长线相交，则截面$BEF$为五边形，棱$DD_1$与平面$BEF$有公共点，因此可得$x+y\geqslant 1$．又$0\leqslant x,y\leqslant 1$，于是$x+y$的取值范围是$[1,2]$．
法二 坐标法
建立空间直角坐标系$D-ACD_1$，则$E(1-x,0,0)$，$B(1,1,0)$，$F(1-y,1,1)$，于是\[\overrightarrow {EB}=(x,1,0),\overrightarrow {FB}=(y,0,-1),\]可得平面$BEF$的法向量为$(-1,x,-y)$，因此平面$BEF$的方程为\[-r+xs-yt=x-1.\]根据题意，当$r=s=0$时，$t\in\left[0,1\right]$，于是$0\leqslant \dfrac{1-x}{y}\leqslant 1$，解得$x+y\geqslant 1$．又$0\leqslant x,y\leqslant 1$，于是$x+y$的取值范围是$[1,2]$．