每日一题[89] 基底思想解向量题

（2015年昆明市第二次统测）三角形$ABC$中，$BC$边上的中垂线分别交$BC$、$AC$于$D$、$M$．若$\overrightarrow{AM}\cdot\overrightarrow{BC}=6$，$AB=2$，则$AC=$_______．

正确答案是$4$．

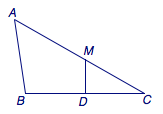
我们将$A$选为基准点，$\overrightarrow{AB}$和$\overrightarrow{AC}$选为基底，分别记为$\overrightarrow a$和$\overrightarrow b$，于是$\overrightarrow{AD}=\dfrac 12\overrightarrow a+\dfrac 12 \overrightarrow b$．设$\overrightarrow{AM}=\lambda \overrightarrow b$．

根据题意，$AB=2$即$\overrightarrow a \cdot \overrightarrow a =4$；

$\overrightarrow{AM}\cdot\overrightarrow{BC}=6$即

$$\lambda \overrightarrow b\cdot\left(\overrightarrow b- \overrightarrow a\right)=6,$$ 整理得 $$\lambda \overrightarrow a\cdot \overrightarrow b=\lambda \overrightarrow b\cdot \overrightarrow b-6.$$

而$MD\perp BC$，于是

$$\left(\dfrac 12\overrightarrow a+\dfrac 12\overrightarrow b-\lambda \overrightarrow b\right)\cdot\left(\overrightarrow b-\overrightarrow a\right)=0,$$ 整理得 $$-\dfrac 12\overrightarrow a\cdot \overrightarrow a+\lambda \overrightarrow a\cdot \overrightarrow b+\left(\dfrac 12-\lambda\right)\overrightarrow b\cdot \overrightarrow b=0,$$ 将之前向量化的已知条件代入，即得 $$\overrightarrow b\cdot \overrightarrow b=16,$$ 从而 $$AC=4.$$