每日一题[792]层层分解

已知函数$f(x)={\rm e}^x\left(2-{\rm e}^x\right)+(a+2)\left|{\rm e}^x-1\right|-a^2$的零点个数为$3$，则实数$a$的取值范围是________．

---

正确答案是$(1,2)$．

分析与解　设$t={\rm e}^x$，且

$$\varphi(t)=t(2-t)+(a+2)\cdot |t-1|-a^2,$$ 根据题意，$\varphi(t)$在$t\in\left(0,+\infty\right)$上有$3$个零点．由于$\varphi(t)$的图象为“m”形，且对称轴为$t=1$，于是必然有 $$\begin{cases}\varphi(0)>0,\\ \varphi(1)<0,\end{cases}$$ 即 $$\begin{cases}a+2-a^2>0,\\ 1-a^2<0,\end{cases}$$ 解得$a$的取值范围是$(1,2)$．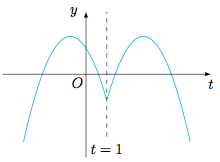

注　也可以将$\varphi(t)$变形为

$$\varphi(t)=-|t-1|^2+(a+2)|t-1|+(1-a^2),$$ 于是考虑函数$g(u)=-u^2+(a+2)u+1-a^2$与$u=|t-1|$的复合函数，知$g(u)$必有两个零点$u_1,u_2$，且$u_1\in(0,1),u_2\geqslant 1$，此时$u_1=|t-1|$有两个根，$u_2=|t-1|$有一个根，满足题意．从而二次函数$g(u)$满足$g(0)<0$且$g(1)>0$．