已知函数$f(x)=x^3+ax^2+bx+c$，$g(x)=3x^2+2ax+b$．若$f(x)$在$(0,1)$上单调递减，则下列结论正确的是________．
(1)$f(0)\cdot f(1)\leqslant 0$；
(2)$g(0)\cdot g(1)\geqslant 0$；
(3)$a^2-3b$有最小值．
正确答案是(2)(3)．
分析与解 因为$g(x)=f'(x)$，所以条件即$g(x)\leqslant 0$在$x\in(0,1)$时恒成立．于是得到命题(1)错误；命题(2)正确．
命题(3)有以下思路．
思路一 $g(0)\leqslant 0$，$g(1)\leqslant 0$，利用规划即得．
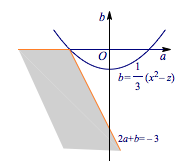记$a^2-3b=z$，考虑抛物线$b=\dfrac 13(a^2-z)$，如图中情形，$z$取到最小值$\dfrac 94$．
思路二 注意到$a^2-3b=\dfrac 14\Delta$，而$$\left|x_1-x_2\right|=\dfrac{\sqrt\Delta}{3},$$再利用$\left|x_1-x_2\right|\geqslant 1$即得．
也即当$0,1$恰好为$g(x)$的两个零点时，$\dfrac 14\Delta $有最小值$\dfrac 94$．
思路三 注意到$g(x)$的开口大小固定（因为$x^2$前系数固定），而$g(x)$的最小值为$-\dfrac 13(a^2-3b)$，所以(3)等价于“$g(x)$的最小值”有最大值，这显然是对的，当$0,1$是$g(x)$的两个零点时，$g(x)$位置达到最高（不能再往$y$轴正方向平移），此时$g(x)$的最小值取到最大值．
思路四 注意到规划边界封闭，因此$a^2-3b$必然存在最小值．