设数列$\{x_n\}$中,$x_1\in (-1,1)$,$x_{n+1}=(-1)^{n+1}\dfrac{3x_n-1}{3-x_n},n\in\mathbb N^*$,若数列$\{x_n\}$的最大值为$x_3$,求$x_1$的取值范围.
分析与解 注意到\[\begin{split} x_{2n+1}&=\dfrac{5x_{2n-1}-3}{3x_{2n-1}-5},\\ x_{2n+2}&=-x_{2n},\end{split}\]为了保证奇数列中$x_3$最大,令$y_n=x_{2n-1}$,则数列$\{y_n\}$的递推公式为$$y_{n+1}=\dfrac {5y_n-3}{3y_n-5},$$可以用两个思路研究$\{y_n\}$:
思路一 利用迭代函数法研究数列的单调性变化
考虑函数$f(x)=\dfrac {5x-3}{3x-5}$,图象如下: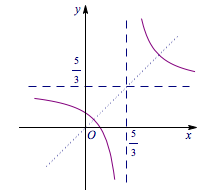 因为$y_1=x_1\in(-1,1)$,且$y_2\geqslant y_1$,即$f(y_1)\geqslant y_1$,结合图象知,$y_1\leqslant \dfrac 13$,即$x_1\leqslant \dfrac 13$.
因为$y_1=x_1\in(-1,1)$,且$y_2\geqslant y_1$,即$f(y_1)\geqslant y_1$,结合图象知,$y_1\leqslant \dfrac 13$,即$x_1\leqslant \dfrac 13$.
由函数$f(x)$的图象关于$y=x$对称知$$y_1=y_3=y_5=\cdots,y_2=y_4=y_6=\cdots,$$从而只需要$x_1\leqslant \dfrac 13$,则有$x_3$为数列的奇数项中的最大项;
注 也可以直接计算得到$$y_3=\dfrac {5y_2-3}{3y_2-5}=\dfrac {5(5y_1-3)-3(3y_1-5)}{3(5y_1-3)-5(3y_1-5)}=y_1.$$
思路二 直接利用不动点法求出通项公式
解方程$\dfrac {5x-3}{3x-5}=x$,得到两个不动点$\dfrac 13,3$,于是我们可以计算得到$$\dfrac {y_{n+1}-3}{y_{n+1}-\frac 13}=-\dfrac {y_n-3}{y_n-\frac 13},$$于是我们有$$\dfrac {y_n-3}{y_n-\frac 13}=(-1)^n\cdot\dfrac {y_1-3}{y_1-\frac 13},$$从而 $\dfrac {y_n-3}{y_n-\frac 13}$在$n$为奇数时为定值,在$n$为偶数时也为定值.
结合函数的单调性知$$y_1=y_3=y_5=\cdots,y_2=y_4=y_6=\cdots,$$于是只需要$y_2\geqslant y_1$,即解方程$$\dfrac {5y_1-3}{3y_1-5}\geqslant y_1,$$即可,解得$y_1=x_1\leqslant \dfrac 13$.
最后考虑偶数项构成的数列:
为了保证$x_3$不小于偶数列中的任意一项,只需要$x_3\geqslant |x_2|$,也即$$\dfrac{5x_1-3}{3x_1-5}\geqslant \left|\dfrac{3x_1-1}{3-x_1}\right|.$$
综上,可得$x_1$的取值范围是$\left(-1,\dfrac 13\right]$.

