(2016年北京市海淀区高三期末考试)已知$f(x)={\rm e}^{-|x|}+\cos \pi x$，给出下列命题：
(1) $f(x)$的最大值为$2$；
(2) $f(x)$在$(-10,10)$内的零点之和为$0$；
(3) $f(x)$的任何一个极大值都大于$1$．
其中，所有正确命题的序号是________．
正确答案是(1)(2)(3)．
分析与解 对于命题(1)，由于\[f(x)={\rm e}^{-|x|}+\cos\pi x\leqslant 2,\]等号当且仅当$x=0$时取得．因此函数$f(x)$的最大值为$2$；
对于命题(2)，由于$f(x)$是偶函数，且在区间$(-10,10)$内存在零点，于是$f(x)$在$(-10,10)$内的零点之和为$0$；
对于命题(3)，显然所有非零整数均不是函数$f(x)$的极值点．而$x=0$是函数$f(x)$的极大值．且有$f(0)=2>1$．考虑到$f(x)$是偶函数，接下来考虑函数$f(x)$在形如$\left(2k,2k+2\right]$($k\in\mathbb N$)的区间内的极值点情况．设$x=t$是函数$f(x)$的极值点，则\[-{\rm e}^{-t}-\pi\sin \pi t=0,\]如图．
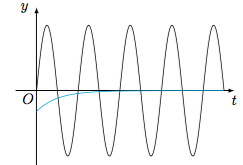由于在区间$(2k,2k+1)$上，有$f'(x)<0$，又\[f'(2k+1)<0,f'\left(2k+\dfrac 32\right)>0,f'(2k+2)<0,\]因此函数$f(x)$在区间$(2k,2k+1)$上不存在极值点，在区间$\left(2k+1,2k+\dfrac 32\right)$上存在一个极小值点，在区间$\left(2k+\dfrac 32,2k+2\right]$上存在一个极大值点．又由于\[f''(x)={\rm e}^{-x}-\pi^2\cos\pi x,\]在区间$(2k+1,2k+2]$上单调递减，于是函数$f''(x)$在区间$(2k+1,2k+2]$内至多只有一个零点，进而函数$f'(x)$在区间$(2k+1,2k+2]$内至多只有两个零点．因此函数$f(x)$在区间$(2k,2k+2]$($k\in\mathbb N$)内的极大值存在且唯一．
另一方面，在每个区间$(2k,2k+2]$($k\in\mathbb N$)内，均存在$x_0=2k+2$．使得\[f(x_0)={\rm e}^{-2k-2}+1>1,\]于是函数$f(x)$的每个极大值都大于$1$．