在三角形\(ABC\)中，\(G\)为重心，且\(AG\perp BG\)，$AB=2$．
（1）求\(\dfrac{1}{\tan A}+\dfrac{1}{\tan B}\)的最小值；
（2）求证：\(\dfrac{\tan C}{\tan A}+\dfrac{\tan C}{\tan B}\)是定值．
正确答案是（1）\(\dfrac 23\)；（2）定值为\(\dfrac 12\)．
取\(AB\)的中点\(M\)，连接\(CG\)、\(GM\)，则易知\(\overrightarrow{MC}=3\overrightarrow{MG}\)．
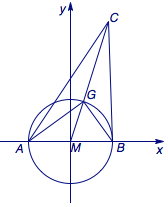
如图建立平面直角坐标系，\(A(-1,0)\)，\(B(1,0)\)，\(G\left(\cos\theta,\sin\theta\right)\)，\(C\left(3\cos\theta,3\sin\theta\right)\)．
此时有\[\begin{split}\tan A&=\dfrac{3\sin\theta}{1+3\cos\theta},\\\tan\left(\pi-B\right)&=\dfrac{3\sin\theta}{1-3\cos\theta}.\end{split}\]
（1）根据上述结果，有\[\dfrac{1}{\tan A}+\dfrac{1}{\tan B}=\dfrac{2}{3\sin\theta}\geqslant \dfrac 23,\]等号当且仅当\(\theta=\dfrac{\pi}2\)时取得．因此所求的最小值为\(\dfrac{2}{3}\)．
（2）根据之前的结果，有\[\begin{split}\dfrac{\tan C}{\tan A}+\dfrac{\tan C}{\tan B}&=\left(\dfrac{1}{\tan A}+\dfrac{1}{\tan B}\right)\cdot \tan \left[\pi-\left(A+B\right)\right]\\&=\left(\dfrac{1}{\tan A}+\dfrac{1}{\tan B}\right)\cdot\left(-\dfrac{\tan A+\tan B}{1-\tan A\cdot\tan B}\right)\\&=\dfrac{1}{2},\end{split}\]为定值．