矩形 $ABCD$中,$AB=4$,$AD=3$,$M,N$分别是线段$BC,CD$上的点,且$\dfrac 1{CM^2}+\dfrac 1{CN^2}=1$,若$\overrightarrow {AC}=x\overrightarrow {AM}+y\overrightarrow {AN}$,则$x+y$的最小值是_________.
分析与解 $\dfrac 54$.
先分析条件中$\dfrac 1{CM^2}+\dfrac 1{CN^2}=1$的含义:
连接$MN$,去分母得到$$CN^2+CM^2=CM^2\cdot CN^2=MN^2,$$于是有$CM\cdot CN=MN$,由三角形$CMN$的面积公式得到$C$到$MN$的距离为$1$,即$MN$是以$C$为圆心,$1$为半径的圆的切线(并不是所有的切线都满足条件,与矩形的边$BC,CD$有交点的才满足条件),记$MN\cap AC=C'$,如图:
由$M,N,C'$三点共线知$\overrightarrow {AC'}=x'\overrightarrow {AM}+y'\overrightarrow {AN}$,其中$x'+y'=1$.从而有$\overrightarrow {AC}=\dfrac {AC}{AC'}\cdot\overrightarrow{AC'}$得到$$x+y=\dfrac {AC}{AC'}=\dfrac 5{AC'}.$$要求$x+y$的最小值即求$AC'$的最大值,由$MN$为圆$C$的切线知,当$C'$在圆$C$上时$AC'$有最大值为$5-1=4$(显然此时$M,N$存在),故所求的最小值为$\dfrac 54$.


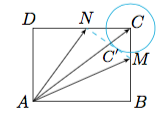
为什么AC'最大值在那里取到??这里不太明白