每日一题[748]复合函数的零点

已知函数$f(x)=-x^2-2x$，$g(x)=\begin{cases} x+\dfrac 1{4x},&x>0,\\ x+1,&x\leqslant 0.\end{cases}$若方程$g(f(x))-a=0$有$4$个实数解，则$a$的取值范围是_______．

分析与解　$\left[1,\dfrac 54\right)$．

函数$y=g(f(x))$可以看成为函数$$y=\begin{cases} t+\dfrac 1{4t},&t>0,\\ t+1,&t\leqslant 0,\end{cases} $$与函数$t=-x^2-2x$复合而成．第一个函数的讨论分界点为$t=0,\dfrac 12$；第二个函数的讨论分界点为$x=-1$．因此总体的讨论分界点为$$x=-2,\dfrac {-2-\sqrt 2}2,-1,\dfrac{-2+\sqrt 2}2,0.$$
根据讨论的分界点，不难得到复合函数在每段上的单调性，再结合分界点处的函数值与渐近线可得复合函数的草图如下：
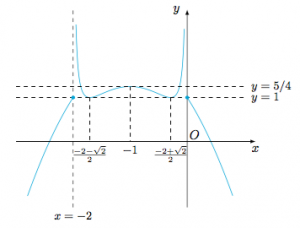由图可得所求$a$的取值范围是$\left[1,\dfrac 54\right)$．

另法　也可以直接分析内外层函数的特点求解，分别作出$f(x),g(x)$的图象知$g(t)=a,t=g(x)$都至多只有两个零点($a,t$为常数)，要使得方程有四个零点，则必然存在$g(t_1)=g(t_2)=a$，且有$f(x_1)=f(x_2)=t_1,f(x_3)=f(x_4)=t_2$．

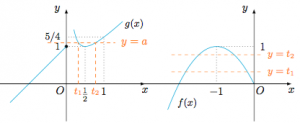因为$f(x)\leqslant 1$，所以$t_1,t_2<1$．而$g(1)=\dfrac 54$，所以$a\in\left[1,\dfrac 54\right)$．