设抛物线$C:y=x^2$的焦点为$F$，动点$P$在直线$l:x-y-2=0$上运动，过点$P$作抛物线$C$的两条切线$PA,PB$且与抛物线分别相切于点$A,B$．
(1) 求$\triangle APB$的重心$G$的轨迹方程；
(2) 求证：$\angle PFA=\angle PFB$．
分析与解 (1) 设$A\left(a,a^2\right)$，$B\left(b,b^2\right)$，则$$PA:y+a^2=2ax,PB:y+b^2=2bx,$$于是$P\left(\dfrac{a+b}2,ab\right)$．设$G(x,y)$，则$$\begin{cases} x=\dfrac13\left(a+b+\dfrac{a+b}2\right)=\dfrac {a+b}{2},\\ y=\dfrac 13\left(a^2+b^2+ab\right),\end{cases} $$又$P$点在直线$x-y-2=0$上，于是$$\dfrac{a+b}2-ab-2=0,$$消去$a+b,ab$，可得所求的轨迹方程为$y=\dfrac 43x^2-\dfrac 13x+\dfrac 23$．
(2)法一 几何性质
分别作焦点$F$关于直线$PA$和$PB$的对称点$F_1$和$F_2$，连接$F_1A,F_1P,F_2B,F_2P,F_1F_2$，如图．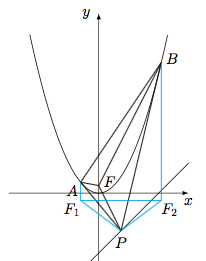
由抛物线的光学性质(因为从焦点射入的直线经抛物线反射后与轴平行，所以$FA$关于切线$AP$的对称直线平行于抛物线的轴)可得$AF_1\parallel OF\parallel BF_2$，$F_1,F_2$均在抛物线的准线上（因为$FA=AF_{1}$，且$AF_1$与$y$轴平行），于是$|PF_1|=|PF|=|PF_2|$，$\angle PF_1F_2=\angle PF_2F_1$，从而$$\angle AF_1P=\angle BF_2P=\angle AFP=\angle BFP,$$原命题得证．
法二 代数计算
由(1)知$F\left(0,\dfrac 14\right)$，$A(a,a^2)$，$B(b,b^2)$，$P\left(\dfrac {a+b}{2},ab\right)$．所以\[\begin{split} \cos\angle PFA=&\dfrac {\overrightarrow {FA}\cdot\overrightarrow {FP}}{\left|\overrightarrow {FA}\right|\cdot\left|\overrightarrow {FP}\right|}\\=&\dfrac{1}{|PF|}\cdot\dfrac{\left(a,a^2-\dfrac 14\right)\cdot\left(\dfrac {a+b}{2},ab-\dfrac 14\right)}{a^2+\dfrac 14}\\=&\dfrac{ab+\dfrac 14}{|PF|}.\end{split} \]同理有$$\cos\angle PFB=\dfrac {ab+\dfrac 14}{|PF|}=\cos\angle PFA,$$从而命题得证．