过双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$($a>0,b>0$)的一个焦点$F$作平行于渐近线的两直线，与双曲线分别交于$A,B$两点，若$|AB|=2a$，双曲线的离心率为$e$，则$\left[e^2\right]=$_______．
答案 $3$．
分析与解 设$\angle AFO =\theta$，则由双曲线的焦半径公式II，有$$|AF|=\dfrac{b^2}{a+c\cdot\cos\theta}=\dfrac{b^2}{2a},$$因此$$\sin\theta=\dfrac{a}{|AF|}=\dfrac{b}{c},$$从而$b^3=2a^2c$，不妨设$a=1$，$c=e$，$b=\sqrt{e^2-1}$，则$$\left(e^2-1\right)^3=4e^2.$$如图，可得$3<e^2<4$，于是$\left[e^2\right]=3$．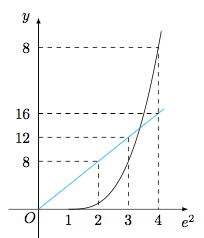
另法 由双曲线的对称性知$AB\perp x$轴，不妨设$A$在$x$轴上方，则$A$点的坐标为$\left(-\dfrac {ac}{b},a\right)$，从而有$$k_{AF}=\dfrac {a}{-\dfrac{ac}{b}+c}=\dfrac ba,$$整理得$$a^2=bc-ac=\sqrt{c^2-a^2}c-ac,$$从而知双曲线的离心率$e$满足$$e^3-e^2-e-1=0.$$记$f(x)=x^3-x^2-x-1$，则$$f'(x)=(x-1)(3x+1),$$所以$f(x)$在$(1,+\infty)$上单调递增，而$$f(\sqrt 3)<0,f(2)>0,$$所以$e\in(\sqrt 3,2)$，从而有$\left[e^2\right]=3$．