2011年高考北京卷理科数学第8题：
设$A(0,0)$，$B(4,0)$，$C(t+4,4)$，$D(t,4)$($t\in\mathcal R$)．记$N(t)$为平行四边形$ABCD$内部(不包含边界)的整点的个数，其中整点是指横坐标和纵坐标都是整数的点，则函数$N(t)$的值域是________．
分析与解 $\{9,11,12\}$．
如图，设直线$y=1$，$y=2$，$y=3$，分别被平行四边形截得的线段为$A_1B_1,A_2B_2,A_3B_3$．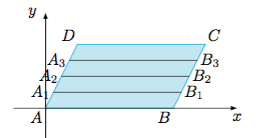
根据题意，$N(t)$就是线段$A_1B_1,A_2B_2,A_3B_3$上(不包含端点)的整点个数之和．区间$(m,m+4)$($m\in\mathcal R$)内的整点个数$$f(m)=\begin{cases} 3,&m\in\mathcal Z,\\ 4,&m\notin \mathcal Z.\end{cases} $$而点$A_1,A_2,A_3$的横坐标分别为$\dfrac 14t,\dfrac 12t,\dfrac {3}{4}t$，于是$$N(t)=f\left(\dfrac 14t\right)+f\left(\dfrac 12t\right)+f\left(\dfrac 34t\right).$$①当$\dfrac 14t,\dfrac 12t,\dfrac {3t}{4}\in\mathcal{Z}$时，$N(t)=9$，此时$t\equiv 0\pmod{4}$，即$t$为$4$的整数倍；
②因为$\dfrac 12t+\dfrac 14t=\dfrac 34t$，所以$\dfrac 14t,\dfrac 12t,\dfrac {3}{4}t$中不可能恰有两个整数，但可能仅有一个是整数，如$t=2$，此时$N(t)=3+4+4=11$．
事实上，当$t\equiv 2\pmod{4}$，即$t=4k+2,k\in\mathcal{Z}$时，$\dfrac 14t,\dfrac 12t,\dfrac {3}{4}t$中恰有一个是整数；当$t=\dfrac 43k$，且$t\notin\mathcal{Z}$时，$\dfrac 14t,\dfrac 12t,\dfrac {3}{4}t$中也恰有一个是整数．
③如果$\dfrac 14t,\dfrac 12t,\dfrac {3}{4}t\notin\mathcal{Z}$时，$N(t)=12$．
综上知，函数$N(t)$的值域是$\{9,11,12\}$．
注 本题原为选择题，省略了选项．