设$S$为半径等于$1$的圆内接三角形的面积，则$4S+\dfrac 9S$的最小值是_______．
分析与解 $7\sqrt 3$．
先证明$S$的最大值为$\dfrac{3\sqrt 3}4$．
设$\triangle ABC$内接于单位圆$O$，且顶点按逆时针排列．设弧$AB,BC,CA$所对的圆心角分别为$\alpha$，$\beta$，$2\pi -\alpha-\beta$，不妨设$\alpha,\beta\in (0,\pi]$，如图：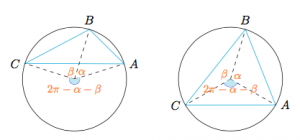
则\[\begin{split} S&=\dfrac 12\left[\sin\alpha+\sin\beta-\sin\left(\alpha+\beta\right)\right]\\&=\dfrac 12\left[\left(1-\cos\beta\right)\sin\alpha-\sin\beta\cos\alpha+\sin\beta\right]\\&\leqslant \dfrac 12\left[\sqrt{(1-\cos\beta)^2+\sin^2\beta}+\sin\beta\right]\\&=\dfrac 12\left[\sqrt{2-2\cos\beta}+\sin\beta\right]\\&=\sin\dfrac{\beta}2\left(1+\cos\dfrac{\beta}2\right),\end{split} \]令$t=1+\cos\dfrac{\beta}2$，则$t\in[1,2)$，有$$S\leqslant t\sqrt{1-(t-1)^2}=\sqrt{t^3(6-3t)}\cdot\dfrac{1}{\sqrt 3}\leqslant \dfrac{3\sqrt 3}4,$$当$\triangle ABC$为正三角形取得等号．
因此$S$的最大值为$\dfrac{3\sqrt 3}4$，而在$\left(0,\dfrac{3\sqrt 3}4\right]$上，$4S+\dfrac{9}S$单调递减，于是所求的最小值为$$\left.\left(4S+\dfrac 9S\right)\right|_{S=\frac{3\sqrt 3}4}=7\sqrt 3.$$