1．已知函数$f(x)=\begin{cases} -x^3-(2a-2)x,&x\leqslant 0,\\ x^3-(3a+3)x^2+ax,&x>0,\end{cases} $若曲线$y=f(x)$在点$P_i(x_i,y_i)$($i=1,2,3$)处的切线互相平行，其中$x_1,x_2,x_3$互不相等，则$a$的取值范围是_______．
2．设非空集合$S=\{x\mid m\leqslant x\leqslant l\}$满足：当$x\in S$时，$x^2\in S$．给出如下三个命题：
(1) 若$m=1$，则$S=\{1\}$；
(2) 若$m=-\dfrac 12$，则$\dfrac 14\leqslant l\leqslant 1$；
(2) 若$l=\dfrac 12$，则$-\dfrac{\sqrt 2}2\leqslant m\leqslant 0$．
其中正确的命题是_______．
3．已知对任意实数$x$，$\sin kx\sin^kx+\cos kx\cos^kx=\cos^k2x$，则整数$k$的值为_______．
4．已知$f(x)=\ln x$，$n$是正整数，求证：$$\displaystyle \dfrac 54n+\dfrac 1{60}<\sum_{k=1}^n\left[2f(2k+1)-f(k)-f(k+1)\right]<2n+1.$$
5．数列$\{a_n\}$满足$a_1=a$，$a_{n+1}=2+a_1a_2\cdots a_n$($n\in\mathcal N^*$)．若使该数列从某项起严格单调递减，则$a$的取值范围是_______．
6．方程$\dfrac{1}{2^{a_1}}+\dfrac{1}{2^{a_2}}+\dfrac{1}{2^{a_3}}+\dfrac{1}{2^{a_4}}+\dfrac{1}{2^{a_5}}+\dfrac{1}{2^{a_6}}=1$的不同正整数解$(a_1,a_2,a_3,a_4,a_5,a_6)$的个数为_______．
7．已知$0<a\leqslant 1$，$x>0$，求证：${\rm e}^{ax}-1+\ln(x+1)>2ax$．
参考答案
1．$\left(-1,+\infty\right)$．
根据已知，$f(x)$的导函数为$$f'(x)=\begin{cases} -3x^2-2a+2,&x<0,\\ 3x^2-6(a+1)x+a,&x>0,\end{cases} $$特别的，如果$a=\dfrac 23$，则有$f'(0)=\dfrac 23$．根据题意，函数$y=f'(x)$的图象与直线$y=m$有$3$个或$3$个以上的公共点．由于左侧的抛物线对称轴恰为$x=0$，于是题意即右侧抛物线的对称轴在$x=0$右侧，且最小值小于$-2a+2$．因此$$\begin{cases} a+1>0,\\ \dfrac{12a-36(a+1)^2}{12}<-2a+2,\end{cases} $$解得$a>-1$．
2．(1)(2)(3)．
根据题意．若$m\leqslant 0$，则$$\begin{cases} m\leqslant 0\leqslant l,\\ m^2\leqslant l,\\ l^2\leqslant l,\end{cases}$$解得$$\begin{cases} m\leqslant 0,\\ m^2\leqslant l\leqslant 1.\end{cases} $$若$m>0$，则$$\begin{cases} 0< m\leqslant l,\\ m^2\geqslant m,\\ l^2\leqslant l,\end{cases}$$解得$$\begin{cases} m=1,\\ l=1.\end{cases} $$对应的区域如图，回到原题，命题(1)(2)(3)正确．
3．$3$．
显然$k\neq 0$．取$x=\dfrac{\pi}k$，则有$$-\cos^k\dfrac{\pi}k=\cos^k\dfrac{2\pi}k,$$显然$k$不是偶数(否则$\cos\dfrac{\pi}k=\cos\dfrac{2\pi}k=0$，无解)，于是$k$为奇数且$$-\cos\dfrac{\pi}k=\cos\dfrac{2\pi}k=2\cos^2\dfrac{\pi}k-1,$$进而$\cos\dfrac{\pi}k=-1$或$\dfrac 12$，进而可得$k=\pm 3$．（$k=1$舍去）
若$k=3$，则\[\begin{split} LHS&=\sin 3x\sin^3x+\cos 3x\cos^3x\\&=\left(3\sin x-4\sin^3x\right)\sin^3x+\left(4\cos^3x-3\cos x\right)\cos^3x\\&=4\cos^6x-3\cos^4x+3\sin^4x-4\sin^6x\\&=4\cos^6x-3\cos^4x\left(\sin^2x+\cos^2x\right)+3\sin^4x\left(\sin^2x+\cos^2x\right)-4\sin^6x\\&=\cos^6x-3\cos^4x\sin^2x+3\cos^2x\sin^4x-\sin^6x\\&=\left(\cos^2x-\sin^2x\right)^3=RHS,\end{split} \]符合题意．
若$k=-3$，则令$x=\dfrac{\pi}4$，则显然$LHS\neq 0=RHS$，不符合题意．
综上所述，整数$k$的值为$3$．
注 由本题条件可得$k>0$，否则$x=\dfrac {\pi}{4}$时，题中等式右边无意义．
4．根据题意，有$$2f(2k+1)-f(k)-f(k+1)=\ln\dfrac{(2k+1)^2}{k(k+1)}=\ln\left(4+\dfrac{1}{k}-\dfrac{1}{k+1}\right),$$而$$\dfrac 54<\ln 4<\ln\left(4+\dfrac{1}{k}-\dfrac{1}{k+1}\right)<\ln 5<2,$$又$k=1$时，有$$\dfrac 54+\dfrac 1{60}<\ln\dfrac 92<3,$$累加即得．
5．$(-2,-1)\cup (-1,0)$．
根据题意，对任意$n\geqslant 2$，$n\in\mathcal N^*$，有$$\begin{cases} a_1a_2\cdots a_{n-1}a_n=a_{n+1}-2,\\ a_1a_2\cdots a_{n-1}=a_n-2,\end{cases} $$于是$$a_{n+1}=a_n^2-2a_n+2,n\geqslant 2,$$而$a_2=2+a$．考虑迭代函数$f(x)=x^2-2x+2$，如图．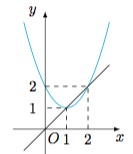
于是只有当$a_2\in (0,1)\cup (1,2)$时，$\{a_n\}$从某项起为单调递减数列．进而可得$a$的取值范围是$(-2,-1)\cup (-1,0)$．
6．$525$．
考虑$a_1\leqslant a_2\leqslant a_3\leqslant a_4\leqslant a_5\leqslant a_6$，则有$$(1,2,3,4,5,5),(1,2,4,4,4,4),(1,3,3,3,4,4),(2,2,2,3,4,4),(2,2,3,3,3,3),$$共$5$组解．于是所求的不同正整数解种数为$$\dfrac{6!}{2!}+\dfrac{6!}{4!}+\dfrac{6!}{3!\cdot 2!}+\dfrac{6!}{3!\cdot 2!}+\dfrac{6!}{2!\cdot 4!}=525.$$
7．原命题等价于$$\forall a\in (0,1],x\in (0,+\infty),{\rm e}^x-1+\ln\left(\dfrac 1ax+1\right)>2x,$$因此只需要证明$$\forall x>0,{\rm e}^x-1+\ln (x+1)>2x.$$事实上，容易证明$$\forall x>0,{\rm e}^x>\dfrac 12x^2+x+1,$$于是$${\rm e}^x-1+\ln(x+1)-2x>\dfrac 12x^2+x+\ln(x+1)-2x,$$记右侧函数为$\varphi(x)$，则其导函数$$\varphi'(x)=x+1+\dfrac{1}{x+1}-2>0,$$于是$\varphi(x)$单调递增，进而当$x>0$时有$$\varphi(x)>\varphi(0)=0,$$原命题得证．