若$\lambda$为实数，若关于$x$的方程$\sqrt{x^2-\lambda}+2\sqrt{x^2-1}=x$有实数解，则$\lambda$的取值范围是______．
分析与解 $\left[0,\dfrac 43\right]$．
法一 设$y=\sqrt{x^2-\lambda}=x-2\sqrt{x^2-1}$，则双曲线$$H_1:x^2-y^2=\lambda$$与双曲线$$H_2:x^2-\dfrac{(x-y)^2}4=1$$在$y\geqslant 0$的半平面有公共点(通过画出双曲线的渐近线$x^2-\dfrac {(x-y)^2}{4}=0$可以很容易得到双曲线的草图)，如图．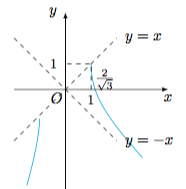
考虑到$H_1$的渐近线为$y=\pm x$，于是$\lambda$的取值范围是$\left[0,\dfrac 43\right]$．
法二 设$$f(x)=\sqrt{x^2-\lambda}+2\sqrt{x^2-1}-x,x\geqslant 1.$$对此函数求导得$$f'(x)=\dfrac {x}{\sqrt{x^2-\lambda}}+\dfrac {2x}{\sqrt{x^2-1}}-1>0,$$于是$f(x)$单调递增．
当$\lambda\leqslant 1$时，$f(1)\leqslant 0$有解，得到$$\sqrt{1-\lambda}-1\leqslant 0,$$解得$\lambda\geqslant 0$；
当$\lambda>1$时，$f(\sqrt{\lambda})\leqslant 0$有解，得到$$2\sqrt{\lambda-1}-\sqrt{\lambda}\leqslant 0,$$解得$\lambda\leqslant \dfrac 43$．
综上知，$\lambda\in\left[0,\dfrac 43\right]$．