设$F$为双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$的左焦点，在$x$轴上$F$点的右侧有一点$A$，以$FA$为直径的圆与双曲线左、右两支在$x$轴上方的交点分别为$M,N$，则$\dfrac{|FN|-|FM|}{|FA|}=$_______．
分析与解 如图．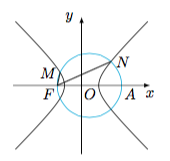
焦半径公式II 设$\angle MFA=\alpha$，$\angle NFA=\beta$，则$$|FM|=\dfrac{b^2}{c\cos\alpha+a},|FN|=\dfrac{b^2}{c\cos\beta-a},$$两式相比可得$$\dfrac{|FM|}{|FN|}=\dfrac{c\cdot \dfrac{|FN|}{|FA|}-a}{c\cdot \dfrac{|FM|}{|FA|}+a}=\dfrac{c|FN|-a|FA|}{c|FM|+a|FA|},$$即$$c|FM|^2+a|FA|\cdot |FM|=c|FN|^2-a|FA|\cdot |FN|,$$也即$$\left(|FM|+|FN|\right)\cdot\left(c|FM|-c|FN|+a|FA|\right)=0,$$从而可得$$\dfrac{|FN|-|FM|}{|FA|}=\dfrac ac.$$
焦半径公式I 设$A(m,0)$($m>-c$)，由圆的直径式方程可得以$FA$为直径的圆的方程为$$(x+c)(x-m)+y^2=0.$$设$M,N$的横坐标分别为$x_1,x_2$，则由焦半径公式，有$$|FM|=-\dfrac cax_1-a,|FN|=\dfrac cax_2+a,$$于是$$\dfrac{|FN|-|FM|}{|FA|}=\dfrac{\dfrac ca\left(x_1+x_2\right)+2a}{m+c}.$$联立圆的方程与双曲线方程，有$$\dfrac{c^2}{a^2}x^2+(c-m)x-cm-b^2=0,$$于是$$x_1+x_2=\dfrac{a^2(m-c)}{c^2},$$代入上式，可得$$\dfrac{|FN|-|FM|}{|FA|}=\dfrac{\dfrac ca\cdot \dfrac{a^2(m-c)}{c^2}+2a}{m+c}=\dfrac ac.$$
注 焦半径公式在方法技巧中有专门介绍．