长为 $3$ 的线段 $AB$ 的两个端点 $A,B$ 分别在 $x$ 轴，$y$ 轴上移动，点 $P$ 在直线 $AB$ 上且满足 $\overrightarrow {BP}=2\overrightarrow {PA}$．
(1) 求点 $P$ 的轨迹方程；
(2) 记点 $P$ 轨迹为曲线 $C$，过点 $Q\left(2,1\right)$ 任作直线 $l$ 交曲线 $C$ 于 $M,N$ 两点，过 $M$ 作斜率为 $-\dfrac{1}{2}$ 的直线 $l'$ 交曲线 $C$ 于另一点 $R$，求证：直线 $NR$ 与直线 $OQ$ 的交点为定点（$O$ 为坐标原点），并求出该定点．
分析与解 (1) 设$P(x,y)$，则$A\left(\dfrac 32x,0\right)$，$B\left(0,3y\right)$，于是由$|AB|=3$可得$$\left(\dfrac 32x\right)^2+\left(3y\right)^2=9,$$即$\dfrac{x^2}4+y^2=1$．
(2) 利用仿射变换$\begin{cases} x'=x,\\ y'= 2y,\end{cases} $将椭圆$E:\dfrac{x^2}4+y^2=1$变为圆$x'^2+y'^2=4$，$Q'(2,2)$，$M'R'$的斜率为$-1$，设直线$N'R'$与直线$OQ'$的交点为$T'$，把问题转化到圆中加以解决，如图．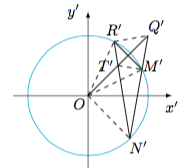
连接$OR',ON',OM',R'Q',M'T'$．由于$OQ'$的斜率为$1$，$R'M'$的斜率为$-1$，于是$OQ'$平分弧$R'M'$，进而可得$$\angle R'OQ'=\angle T'OM'=\angle R'N'M',$$于是$O,R',Q',N'$四点共圆，$O,T',M',N'$四点共圆，有$$\angle R'Q'O=\angle ON'R'=\angle OM'T'=\angle OR'T',$$从而$\triangle OT'R'$与$\triangle OR'Q'$相似，有$$|OT'|\cdot |OQ'|=|OR'|^2=4,$$因此$|OT'|$为定值$\sqrt 2$，$T'$为定点$(1,1)$．转化到原坐标，所求定点$T$为$\left(1,\dfrac 12\right)$．