每日一题[76] 正方体中的不变量

在正方体\(ABCD-A'B'C'D'\)中，若点\(P\)（异于点\(B\)）是棱上一点，则满足\(BP\)和\(AC'\)所成的角为\(45^\circ\)的点\(P\)的个数为______．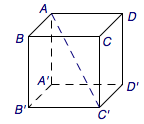

正确答案是\(3\)． 如图，当动点\(M\)在直线上运动时，直线\(PM\)与某固定方向所成的角会先由\(0\circ\)（无法取得）增大到\(90^\circ\)然后减小到\(0^\circ\)（无法取得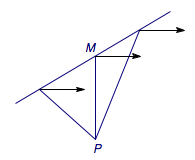）． 于是我们可以将正方体的各个顶点（除\(B\)点外）染色，当顶点与\(B\)的连线与直线\(AC'\)所成的角大于等于\(45^\circ\)时染为红色，否则染为蓝色，如下图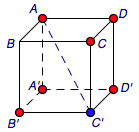． 当某条棱的两个端点为一红一蓝时，根据零点的存在性定理与之前的论述，该棱上存在唯一一个符合题意的点；当某条棱的两个端点均为红色时，该棱上不存在符合题意的点；当某条棱的两个端点均为蓝色时，需要仔细考虑． 综上，符合题意的点共有\(3\)个，分别位于棱\(B'C'\)、\(CC'\)、\(C'D'\)上．