每日一题[573]丝丝入扣

已知对任意$x\in [0,1]$，均有$\big|ax^2+bx+c\big|\leqslant 1$，求$\big|cx^2+bx+a\big|$在$[0,1]$上的最大值．

---

分析与解　设$f(x)=ax^2+bx+c$，则

$$\begin{cases} f(0)=c,\\ f\left(\dfrac 12\right)=\dfrac 14a+\dfrac 12b+c,\\ f(1)=a+b+c,\end{cases}$$ 解得 $$\begin{cases} a=2f(0)+2f(1)-4f\left(\dfrac 12\right),\\ b=4f\left(\dfrac 12\right)-3f(0)-f(1),\\ c=f(0),\end{cases}$$ 于是当$x\in [0,1]$时，有 $$\begin{split} \big|cx^2+bx+a\big|-\big|ax^2+bx+c\big|&\leqslant \big|cx^2+bx+a-(ax^2+bx+c)\big|\\ &=\big|(a-c)(1-x^2)\big| \leqslant \big|a-c\big| \\ &=\left|f(0)+2f(1)-4f\left(\dfrac 12\right)\right|\\ &\leqslant \big|f(0)\big|+2\big|f(1)\big|+4\left|f\left(\dfrac 12\right)\right| \\&\leqslant 7,\end{split}$$ 因此有 $$\big|cx^2+bx+a\big|\leqslant 7+\big|ax^2+bx+c\big|\leqslant 8,$$ 事实上，取$a=8,b=-8,c=1,x=0$可得$\big|cx^2+bx+a\big|=8$，因此所求的最大值为$8$．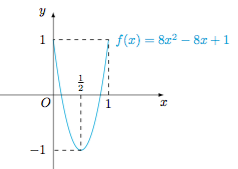
思考与总结　利用特殊位置的点(通常为区间端点及极值点)处的函数值表示多项式的系数，然后利用绝对值不等式求解对应的最值问题是解决此类问题的常见思路．把$x$看成是“权重”有助于更好的理解本题的解题思路．

类似问题见每日一题[436]我家住着抛物线．