每日一题[69] 抽象函数

已知函数$f(x)$的定义域为$\mathcal R$，且满足：

① $f(1)=2$；

② $\forall x,y\in\mathcal R,f(x+y+1)=f(x-y+1)-f(x)f(y)$；

③ $f(x)$在区间$[0,1]$上单调递增．

（1）求$f(0)$，$f(-1)$；

（2）求$f(x)$的零点；

（3）解不等式：$f(x)>1$．

---

（1）解    在②中，令$x=1$得

$$f(y+2)=f(2-y)-2f(y),$$ 令$y=1$得 $$f(x+2)=-f(x),$$ 于是可得 $$f(x+2)=-f(x),f(-x)=-f(x).$$

由此可得$f(0)=0$，$f(-1)=-2$．

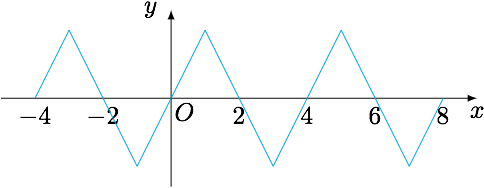
（2）解    由函数$f(x)$为奇函数，且为类周期函数，结合③有函数的草图如下：

因此函数$f(x)$的零点为$x=2k,k\in\mathcal Z$．

（3）解    令$y=-x$有

$$f(2x+1)+f^2(x)=2,$$ 设$f(m)=1,m\in (0,1)$，则 $$f(2m+1)=1.$$

于是由函数的周期性与单调性，有

$$2m+1=m+4k\lor 2m+1=2-m+4k,$$ 其中$k\in\mathcal Z$．

不难解得

$$m=\dfrac 13.$$

因此所求不等式的解为

$$\bigcup_{k\in\mathcal Z}\left(\dfrac 13+4k,\dfrac 53+4k\right),k\in\mathcal Z.$$