每日一题[458]运动中的不变量

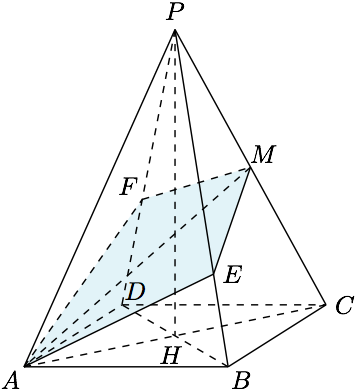
设$P-ABCD$是一个高为$3$，底面边长为$2$的正四棱锥，$M$是棱$PC$的中点，过$AM$作平面与线段$PB,PD$分别交于$E,F$（可以是线段的端点）．试求四棱锥$P-AEMF$的体积的最大值与最小值．

分析    注意到$A,M$为定点，于是有$$V_{P-AEMF}=V_{A-PEF}+V_{M-PEF}=\dfrac 13\cdot \dfrac 32AH\cdot S_{\triangle PEF},$$因此只需要考虑$S_{\triangle PFE}$的取值范围．

解    根据题意，$AM$与$PH$的交点$G$为$\triangle PAC$的重心，也为$\triangle PBD$的重心．设$\overrightarrow {PF}=\lambda \overrightarrow{PD}$，$\overrightarrow{PE}=\mu \overrightarrow{PB}$，其中$\lambda,\mu\in (0,1]$，则$$S_{\triangle PFE}=\lambda \mu S_{\triangle PBD},$$由向量知识不难得到$$\dfrac{1}{\lambda}+\dfrac{1}{\mu}=3,$$因此$\lambda\mu$的取值范围是$\left[\dfrac 49,\dfrac 12\right]$，进而$V_{P-AEMF}$的取值范围是$$\left[\dfrac 29\cdot AH\cdot S_{\triangle PBD},\dfrac 14\cdot AH\cdot S_{\triangle PBD}\right].$$考虑到$$ V_{P-ABCD}=\dfrac 23 AH\cdot S_{\triangle PBD}=4,$$于是$$AH\cdot S_{\triangle PBD}=6,$$所求的取值范围为$\left[\dfrac 43,\dfrac 32\right]$．