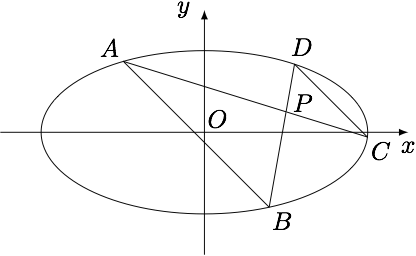
已知过点$P\left(1,\dfrac 14\right)$的直线$l_1,l_2$分别与椭圆$\dfrac{x^2}4+y^2=1$相交于点$A,C$与$B,D$,且$\overrightarrow{AP}=2\overrightarrow{PC}$,$\overrightarrow{BP}=2\overrightarrow{PD}$,求直线$AB$的方程.
解 设$A(x_1,y_1)$,$C(x_2,y_2)$,则\[\begin{cases} x_2=\dfrac{3\cdot 1-x_1}{2},\\ y_2=\dfrac{3\cdot \dfrac 14-y_1}{2},\end{cases} \]于是$$\dfrac{\left(\dfrac{3-x_1}2\right)^2}4+\left(\dfrac{\dfrac 34-y_1}{2}\right)^2=1,$$即$$\dfrac{x_1^2}4+y_1^2-\dfrac 32x_1-\dfrac 32y_1-\dfrac {19}{16}=0,$$也即$$x_1+y_1+\dfrac 18=0.$$类似的,点$B(x_3,y_3)$的坐标也满足$$x_3+y_3+\dfrac 18=0,$$因此直线$AB$的方程为$$x+y+\dfrac 18=0.$$
注 当然,用同样的方法,可以求出直线$CD$的方程为$$x+y-\dfrac{31}{16}=0.$$