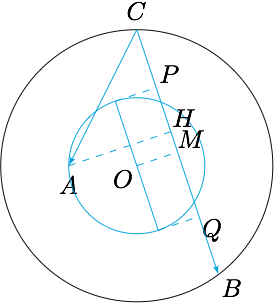
如图,圆$O$的半径为$1$,$OA=\dfrac 12$.设$B,C$是圆$O$上任意两点,则$\overrightarrow{AC}\cdot\overrightarrow{BC}$的取值范围是_______.
分析 注意到$\overrightarrow{AC}\cdot\overrightarrow{BC}=\overrightarrow{CA}\cdot \overrightarrow{CB}$,因此选择以$C$为起点进行研究.此时$A,B$分别在半径为$\dfrac 12,1$的圆上运动.
解 先固定$\overrightarrow{CB}$.
如图,设$A,O$在$CB$上的投影分别为$H,M$,以$O$为圆心,$\dfrac 12$为半径的圆在$CB$上的投影为线段$PQ$,则$$\overrightarrow{CA}\cdot\overrightarrow{CB}=\overrightarrow{CH}\cdot \overrightarrow{CB}=\left(\overrightarrow{CM}+\overrightarrow{MH}\right)\cdot \overrightarrow{CB}=\dfrac 12 CB^2+\overrightarrow{MH}\cdot\overrightarrow{CB}.$$考虑到$H$在线段$PQ$上,于是$\overrightarrow{CA}\cdot\overrightarrow{CB}$的最大值为$$\dfrac 12CB^2+\dfrac 12CB,$$最小值为$$\dfrac 12CB^2-\dfrac 12CB.$$
接下来放开$\overrightarrow{CB}$,有$0\leqslant CB\leqslant 2$,于是$\overrightarrow{CA}\cdot\overrightarrow{CB}$的最大值为$3$,最小值为$-\dfrac 18$.
另法 统一起点为$O$,则\[\begin{split} \overrightarrow{AC}\cdot \overrightarrow{BC}& = \left(\overrightarrow{OC}-\overrightarrow{OA}\right)\cdot \left(\overrightarrow{OC}-\overrightarrow{OB}\right) \\ &=OC^2-\overrightarrow{OA}\cdot \overrightarrow{OC}+\overrightarrow{OA}\cdot\overrightarrow{OB}-\overrightarrow{OC}\cdot\overrightarrow{OB} \\ &=OC^2+\dfrac 12\left[\left(\overrightarrow{OA}+\overrightarrow{OB}-\overrightarrow{OC}\right)^2-OA^2-OB^2-OC^2\right] \\ &=\dfrac 12\left(\overrightarrow{OA}+\overrightarrow{OB}-\overrightarrow{OC}\right)^2-\dfrac 18,\end{split} \]考虑到$\overrightarrow{OB}-\overrightarrow{OC}$可以表示长度从$0$到$2$的任意向量,因此$\overrightarrow{OA}+\overrightarrow{OB}-\overrightarrow{OC}$的长度取值范围是$\left[0,\dfrac 52\right]$,所求的取值范围是$\left[-\dfrac 18,3\right]$.