每日一题[58] 切线—联结椭圆与圆的纽带

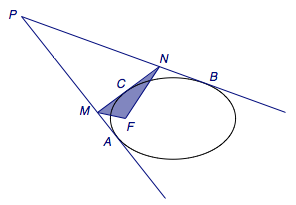
如图，过椭圆外一点引椭圆的两条切线\(PA\)与\(PB\)．椭圆上一点\(C\)处的切线与\(PA\)、\(PB\)分别交于\(M\)、\(N\)，即椭圆与三角形\(PMN\)旁切．求证：\(MN\)对椭圆的焦点\(F\)的张角大小与\(C\)点的位置无关．

我们有一个椭圆的切线相关的重要辅助线及其性质：作椭圆的某个焦点关于切线的对称点，那么该点位于另一焦点与切点所在的直线上（三点共线）且该点到另一焦点的距离为椭圆的长轴长（位于以另一焦点为圆心，长轴长为半径的圆上）．

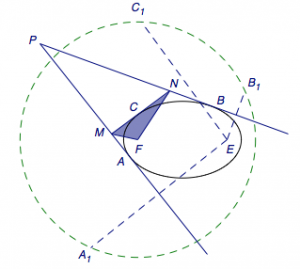
在本题中，设椭圆的另一个焦点为\(E\)，以\(F\)为圆心，长轴长为半径作圆，则\(E\)点关于\(PA\)、\(PB\)、\(MN\)的对称点\(A_1\)、\(B_1\)、\(C_1\)均在圆上，如图．

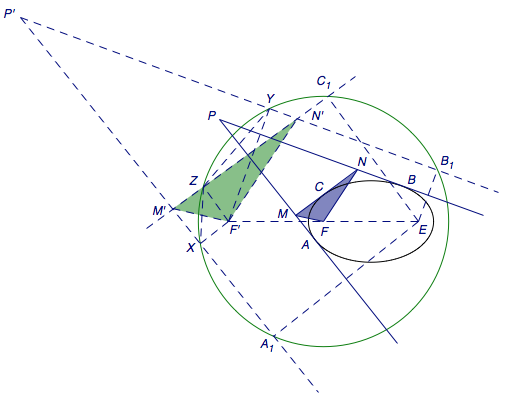
接下来想办法将\(\angle MFN\)从难处理的椭圆中转移到容易处理的圆中．如图，过\(A_1\)、\(B_1\)、\(C_1\)分别作直线\(P'A_1\)、\(P'B_1\)、\(M'N'\)与直线\(PA\)、\(PB\)、\(MN\)平行，这相当于以\(E\)为中心，将\(PMA\)、\(PNB\)放大到原来的两倍．因此类似的将\(F\)放大到\(F'\)的位置，其中\(F'E=2FE\)．这样就有\(\angle MFN=\angle M'F'N'\)．

最后我们集中精力在圆中解决这个问题（如下图）．

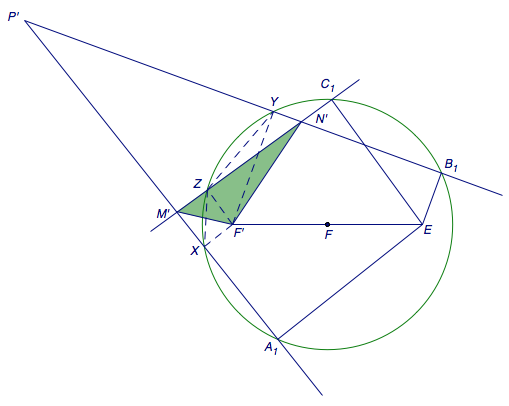设\(P'A_1\)、\(P'B_1\)、\(M'N'\)分别与圆交于点\(X\)、\(Y\)、\(Z\)，连接\(F'X\)、\(F'Y\)、\(F'Z\)、\(ZX\)、\(ZY\)．

由于\(F\)平分\(F'E\)且为圆心，于是\(F'X\perp P'A_1\)、\(F'Y\perp P'B_1\)、\(F'Z\perp M'N'\)，进而\(Z,M',X,F'\)四点共圆，\(Z,Y,N',F'\)四点共圆．

于是所求角\[\begin{split}\angle M'F'N'&=\angle M'F'Z+\angle N'F'Z\\&=\angle M'XZ+\left(\pi-\angle ZYB_1\right)\\&=\pi-\angle A_1XZ+\pi-\angle ZYB_1\end{split}\]

因此\(M'F'N'\)的大小始终为弧\(A_1C_1B_1\)所对的圆周角，与\(C_1\)的位置无关．进而\(MFN\)的大小是固定的，而与\(C\)的位置无关，原命题得证．

最后给出所有辅助线的“全家福”．