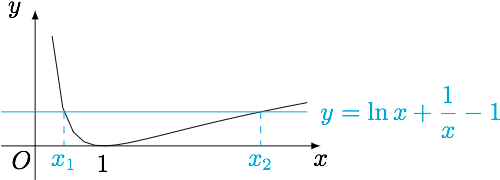
已知$f(x)=x-1-\ln x$,若两相异正实数$x_1,x_2$满足$f(x_1)=f(x_2)$,求证:$f'(x_1)+f'(x_2)<0$.
证明 由于$f(x)$的导函数$$f'(x)=1-\dfrac 1x,$$于是欲证不等式即$\dfrac{1}{x_1}+\dfrac{1}{x_2}>2$.
问题转化为
已知$g(x)=f\left(\dfrac 1x\right )=\ln x+\dfrac 1x-1$,若实数$x_1,x_2$满足$0<x_1<1<x_2$且$g(x_1)=g(x_2)$,求证:$x_1+x_2>2$.
我们利用对称化构造辅助命题:$$\forall x\in (0,1),g(1+x)<g(1-x).$$
引理的证明是容易的,令函数$$h(x)=\ln{(1-x)}+\dfrac{1}{1-x}-\ln{(1+x)}-\dfrac{1}{1+x},$$则其导函数$$h'(x)=\dfrac{x}{(1-x)^2}-\dfrac{x}{(1+x)^2}>0,$$而$h(0)=0$,于是$h(x)>0$,即辅助命题得证.
应用辅助命题我们有$$g(x_2)=g(x_1)=g[1-(1-x_1)]>g(2-x_1),$$而$g(x)$在$(1,+\infty)$上单调递增,于是$x_2>2-x_1$,即$$x_1+x_2>2,$$从而原命题得证.
注 也可以用换元法或A-L-G不等式证明.