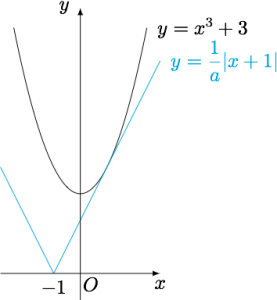本题是一个学生的问题:
已知不等式$ax^2-|x+1|+3a\geqslant 0$的解集为$\mathcal R$,求$a$的取值范围.
正确答案是$\left[\dfrac 12,+\infty\right )$.
分析 问题等价于$$\forall x\in\mathcal R,ax^2-|x+1|+3a\geqslant 0,$$这种含参的不等式或方程问题中对参数的处理一般有全分离、半分离、不分离的三种方式.
解法一 全分离
问题等价于$$\forall x\in\mathcal R,a\geqslant \dfrac{|x+1|}{x^2+3},$$令$x+1=t$,则右边即$\dfrac{|t|}{t^2-2t+4}$,记为$f(t)$.由$$f(t)=\begin{cases} \dfrac{1}{t+\frac 4t-2},&t>0,\\ 0,&t=0,\\ -\dfrac{1}{t+\frac 4t-2},&t<0,\end{cases} $$可得$f(t)$的值域为$\left[0,\dfrac 12\right]$.因此$a$的取值范围是$\left[\dfrac 12,+\infty \right)$.
解法二 半分离
显然$a\neq 0$,于是问题等价于$$\forall x\in\mathcal R,x^2+3\geqslant \dfrac 1a\cdot |x+1|,$$如图.计算可知极限情况时$\dfrac 1a=2$,因此可得$a$的取值范围是$\left[\dfrac 12,+\infty \right)$.
解法三 不分离
此时需要一个小技巧:$\min\{a,b\}\geqslant c$等价于$a\geqslant c$且$b\geqslant c$.
原题即$$\begin{cases} \forall x\in\mathcal R,ax^2-(x+1)+3a\geqslant 0,\\ \forall x\in\mathcal R,ax^2+(x+1)+3a\geqslant 0,\end{cases} $$即$$\begin{cases} \forall x\in\mathcal R,ax^2-x+3a-1\geqslant 0,\\ \forall x\in\mathcal R,ax^2+x+3a+1\geqslant 0,\end{cases} $$于是$$\begin{cases} a>0,\\ 1-4a(3a-1)\leqslant 0,\end{cases} \land \begin{cases} a>0,\\ 1-4a(3a+1)\leqslant 0,\end{cases} $$解得$a\geqslant \dfrac 12$,于是$a$的取值范围是$\left[\dfrac 12,+\infty \right)$.
注 解法一中,分离后也可以直接通过$$f(t)=\dfrac{1}{|t|+\dfrac{4}{|t|}-2\dfrac{t}{|t|}},$$由分母的最小值为$2$,得到$f(t)$的最大值为$\dfrac 12$.
更多相关问题见每日一题[234]分离变量、每日一题[299]分段与分离相遇.