每日一题[421]空间向量的分解

这是我在QQ群（我也记不得是哪个了）里看到的问题：

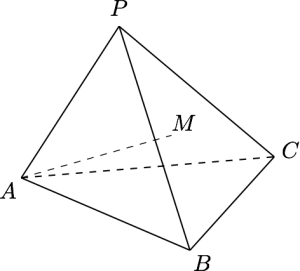
如图，在三棱锥$P-ABC$中，$AB=AC=PB=PC=10$，$PA=8$，$BC=12$，点$M$在平面$PBC$内，且$AM=7$，设异面直线$AM$与$BC$所成角为$\alpha$，则$\cos\alpha$的最大值为_______．

---

正确答案是$\dfrac 17$．

分析    首先确定$M$点可能的位置．由于$AM$是定长线段，因此$M$的轨迹是平面$PBC$上的圆，圆心为$A$在平面$PBC$上的投影，如图．

接下来可以利用空间向量求$\cos\alpha$的最大值，利用$M$点的轨迹的形成方式对向量$\overrightarrow{AM}$进行适当的分解是解决问题的关键．

解    利用图形的对称性，取$BC$的中点$N$，连接$PN,AN$．不难计算得

$$AN=PN=8,$$ 于是三角形$PAN$为正三角形，记$H$为点$A$在平面$PBC$上的投影，则$AH=4\sqrt 3$．因此点$M$的轨迹是半径为 $$\sqrt{AM^2-AH^2}=1$$ 的圆，这样就有 $$\cos\alpha=\left|\dfrac{\overrightarrow{AM}\cdot \overrightarrow{BC}}{AM\cdot BC}\right|=\left|\dfrac{\overrightarrow{AH}\cdot \overrightarrow{BC}+\overrightarrow{HM}\cdot \overrightarrow{BC}}{AM\cdot BC}\right|,$$ 注意到$AH\perp BC$，于是 $$\overrightarrow{AH}\cdot\overrightarrow{BC}=0,$$ 而$\overrightarrow{HM}$与$\overrightarrow{BC}$的夹角取值范围是$[0,\pi]$，因此$\cos\alpha$的最大值为 $$\dfrac{HM\cdot BC}{AM\cdot BC}=\dfrac 17.$$

---

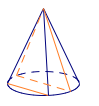
注　从立体几何角度来看，因为$AM$是母线长为$7$，底面半径为$1$的圆锥上的任意一条母线，$BC$可以平移到底面上，成为一条弦，要找到一条母线，使得该母线与弦的夹角的最小值．

因为任意一条弦与两条母线构成腰为$7$的等腰三角形，故顶角最大时，底角最小，即将$BC$平移到直径位置时，对应的底角有最小值．