已知函数$f(x)=\left \lvert x^2-ax \right \rvert -2$,且函数$f(x+2)$是偶函数.
(1)求实数$a$的值;
(2)设函数$y=g(x)$,集合$M=\{x|g(x)-x=0\},N=\{x|g(g(x))-x=0\}$.
① 证明$M\subseteq N$;
② 如果$g(x)=f(\lvert x \rvert )$,集合$P=\{x|g(g(x))-x=0\land \lvert x \rvert \leqslant 2 \}$,那么集合$P$中的元素个数为_______.
正确答案是(1)$a=4$;(2)①略;②$5$.
解 直接看(2)的②,直接求解方程$g(g(x))=x$显然不明智,如果考虑数形结合,那么函数$g(g(x))$的图象也并不好画.难点主要在于$$g(g(x))=x$$这个式子的左边“穿的衣服”有点多,跟式子的右边形成了鲜明的对比.不患寡而患不均啊!能否脱掉左边的一件衣服给右边穿呢?我们先来证明一个引理:
方程$g(g(x))=x$的根为曲线$y=g(x)$与曲线$x=g(y)$(这两条曲线关于直线$y=x$对称)的交点的横坐标.
证明 一方面,设$a$是方程$g(g(x))=x$的一个根,即$g(g(a))=a$.
设$g(a)=b$,则$g(b)=g(g(a))=a$,故点$(a,b)$既在曲线$y=g(x)$上,又在曲线$x=g(y)$上,所以$a$是曲线$y=g(x)$与曲线$x=g(y)$的交点的横坐标.
另一方面,设曲线$y=g(x)$与曲线$x=g(y)$的一个交点为$(a,b)$,则$g(a)=b$,且$g(b)=a$.
故$g(g(a))=g(b)=a$,所以$a$是方程$g(g(x))=x$的一个根.
证毕.
注意 方程$g(g(x))=x$的根有可能不存在,对应的,曲线$y=g(x)$与曲线$x=g(y)$的交点也有可能不存在.
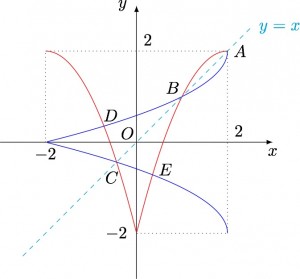
下面我们用这个引理来解决此题:作出曲线$y=g(x)$(红色实线)与曲线$x=g(y)$(蓝色实线),这两条曲线关于直线$y=x$(青色虚线)对称,如下图所示.
从图中可以看到,红色实线与蓝色实线共有$A,B,C,D,E$这$5$个交点,所以集合$P$中的元素个数为$5$.