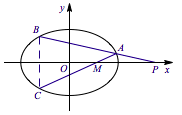
已知椭圆$\dfrac {x^2}{4}+\dfrac {y^2}{3}=1$,点$P(4,0)$,过点$P$作椭圆的割线$PAB$,$C$为$B$关于$x$轴的对称点.求证:直线$AC$恒过定点.
解 因为$A,B,P$三点共线,$A,C,M$三点也共线,且$A,B,C$三点都在椭圆上,我们用定比点差法去解决这个问题.
设$A(x_1,y_1)$,$B(x_2,y_2)$,则$C(x_2,-y_2)$,设$AC$与$x$轴的交点为$M(m,0)$,$\overrightarrow {AP}=\lambda \overrightarrow {PB}$,$\overrightarrow {AM}=\mu\overrightarrow {MC}$,则\[P\left(\dfrac {x_1+\lambda x_2}{1+\lambda },\dfrac {y_1+\lambda y_2}{1+\lambda }\right ),M\left(\dfrac {x_1+\mu x_2}{1+\mu },\dfrac {y_1-\mu y_2}{1+\mu}\right ).\]于是有\[\begin{split}\begin{eqnarray} x_1+\lambda x_2=4(1+\lambda ),y_1+\lambda y_2=0;\\x_1+\mu x_2=m(1+\mu),y_1-\mu y_2=0.\end{eqnarray} \end{split} \]由点$A,B$在椭圆上得\[\begin{cases} \dfrac {x_1^2}{4}+\dfrac {y_1^2}{3}=1,\\\dfrac {\mu^2x_2^2}{4}+\dfrac {\mu^2y_2^2}{3}=\mu^2.\end{cases} \]两式相减得\[\begin{eqnarray} \dfrac {(x_1+\mu x_2)(x_1-\mu x_2)}{4}+\dfrac {(y_1+\mu y_2)(y_1-\mu y_2)}{3}=1-\mu ^2.\end{eqnarray} \]将(2)代入(3)得\[\begin{eqnarray} x_1-\mu x_2=\dfrac {4(1-\mu)}{m}.\end{eqnarray} \]由(1)(2)得$\mu=-\lambda $,代入(4)得\[x_1+\lambda x_2=\dfrac {4(1+\lambda )}{m}.\]与(1)对比得$m=1$,即直线$AC$恒过定点$(1,0)$.
定比点差法处理有心二心曲线的三点共线问题非常有效,更多相关问题见每日一题[327]定比点差法,每日一题[181]定比点差法.详细的定比点差法介绍见[方法技巧]点比定差法.