每日一题[327]定比点差法

2015年高考数学北京文科第20题（解答压轴题）：

已知椭圆$C:x^2+3y^2=3$，过点$D(1,0)$且不过点$E(2,1)$的直线与椭圆$C$交于$A$，$B$两点，直线$AE$与直线$x=3$交于点$M$．

(1)求椭圆$C$的离心率；

(2)若$AB$垂直于$x$轴，求直线$BM$的斜率；

(3)试判断直线$BM$与直线$DE$的位置关系，并说明理由．

---

正确答案是（1）$\dfrac{\sqrt 6}3$；（2）$1$；（3）平行．

分析　第（1）（2）小题比较常规，略去，重点看第（3）小题．从第(2)小题给出的特殊情形可以猜测第(3)小题中$BM$与$DE$平行，再去证明． 常规的证明方式是设出直线$AB$的斜率，联立直线与椭圆的方程消去一个参数，得到$A,B$的横坐标（或纵坐标）满足的方程，再用$A,B$的坐标表达出$M$点的坐标，去证明$DE$与$BM$的斜率相等．这种方式的本质是引入直线$AB$的斜率作为参数，去表达直线与椭圆相交这样的关系，通过联立去进行消参，这也是圆锥曲线问题的一个比较常规的处理方式．但引入参数方式并不唯一，只要能达到消参的目的，同时能很好地表达题目中的条件与结论就是好参数． 下面给出另外一种设参思路，帮助我们看清设参的本质，本题关键条件有：$A,D,B$三点共线，$A,E,M$三点共线，$A,B$两点在椭圆上．解题的关键是要表达出这三个条件，并且方便证明$DE\parallel BM$，于是直接引入线段比作为参数．

解　(3)直线$BM$与$DE$平行，证明如下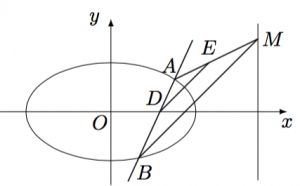． 设$\overrightarrow {AD}=\lambda \overrightarrow {DB}$，$A(x_1,y_1)$，$B(x_2,y_2)$，则

$$D\left(\dfrac{x_1+\lambda x_2}{1+\lambda},\dfrac{y_1 + \lambda y_2}{1+ \lambda}\right)=(1,0),$$ 于是 $$\begin{cases} x_1+\lambda x_2=1+\lambda,\\y_1+\lambda y_2=0.\end{cases}$$ 由已知，有 $$\begin{cases} x_1^2+3y_1^2=3,\\\lambda^2x_2^2+3\lambda^2y_2^2=3\lambda^2,\end{cases}$$ 两式相减得 $$(x_1+\lambda x_2)(x_1-\lambda x_2)+3(y_1+\lambda y_2)(y_1-\lambda y_2)=3(1+\lambda)(1-\lambda),$$ 应用$D$点坐标，可得 $$x_1-\lambda x_2=3-3\lambda,$$ 进而 $$x_1=2-\lambda.$$ 于是 $$\dfrac{AE}{EM}=\dfrac{2-x_1}{3-2}=\lambda,$$ 根据平行线截割定理的逆定理可知，直线$DE$与直线$BM$平行． 本题的方法是处理与中点相关的问题的“点差法”的升华，称为“定比点差法”．