每日一题[337]单刀直入

已知满足条件$x^2+y^2\leqslant 1$的点$(x,y)$构成的平面区域的面积为$S_1$，满足条件$[x]^2+[y]^2\leqslant 1$的点$(x,y)$构成的平面区域的面积为$S_2$（其中$[x],[y]$分别表示不超过$x,y$的最大整数），则$S_1$与$S_2$的大小关系是______．

正确答案是$S_1<S_2$．

解　问题的难点在于如何将约束条件 $$[x]^2+[y]^2\leqslant 1$$ 几何化．考虑到$[x]$与$[y]$均为整数，于是可以分类讨论：

1）$[x]=-1$时，$[y]=0$；

2）$[x]=0$时，$[y]=-1,0,1$；

3）$[x]=1$时，$[y]=0$．

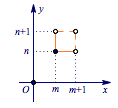
而当$[x]=k$时，有 $$k\leqslant x<k+1,$$ 从而每个整点$(m,n)$（其中$[x]=m,[y]=n$）对应这个点右上方的小正方形，如图：

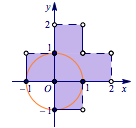
于是得到满足条件$[x]^2+[y]^2\leqslant 1$的点$(x,y)$构成的平面区域如下：

容易得到$S_1=\pi<S_2=5$．

在数据比较小时，直接对复杂条件进行分类讨论也是一种值得尝试的方式，简单有效．

下面给出一道练习：

若集合$P=\{0,1,2\}$，集合$Q=\left\{(x,y)\left|\begin{cases} x-y+1>0,\\x-y-2<0,\end{cases} \right.x,y\in P\right \}$，则$Q$中元素的个数是____．

答案　$5$．

提示　集合$Q$中的$y$满足$x-2<y<x+1$，即$x-1\leqslant y\leqslant x$，直接按$x=0,1,2$分类讨论即可．