2015年高考数学重庆卷文科第22题（解答压轴题）：
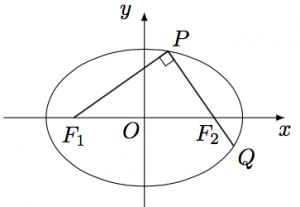
如图，椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为$F_1$，$F_2$，过$F_2$的直线交椭圆于$P$，$Q$两点，且$PQ\perp PF_1$．若 ${\left|{PQ}\right|}=\lambda {\left|{PF_1}\right|}$，且$\dfrac 34\leqslant \lambda<\dfrac 43$，试确定椭圆离心率$e$的取值范围．
正确答案是$\left(\dfrac{\sqrt 2}2,\dfrac{\sqrt 5}3\right]$．
解 连接$QF_1$，并设$|PF_1|=m$，$|PF_2|=n$．
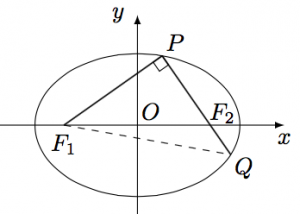由$\triangle PF_1Q$是直角三角形得$$|QF_2|=\lambda m-n,|QF_1|=\sqrt {1+\lambda^2}m.$$
由椭圆的定义，有$$|PF_1|+|PF_2|=|QF_1|+|QF_2|,$$即$$m+n=\sqrt {1+\lambda^2}m+(\lambda m-n),$$从而$$\dfrac nm=\dfrac 12\left(\lambda -1+\sqrt{1+\lambda^2}\right).$$
当$\lambda \in\left[\dfrac 34,\dfrac 43\right)$时，由于$\dfrac nm$随着$\lambda$的增大而增大，于是$\dfrac nm$的取值范围是$\left[\dfrac 12,1\right)$．
进而椭圆的离心率$$e=\dfrac{2c}{2a}=\dfrac{|F_1F_2|}{|PF_1|+|PF_2|}=\dfrac{\sqrt{m^2+n^2}}{m+n}=\sqrt{\dfrac{1}{1+\dfrac{2}{\frac mn+\frac nm}}},$$我们熟知函数$y=x+\dfrac 1x$在区间$(0,1)$上单调递减，因此当$\dfrac nm\in\left[\dfrac 12,1\right)$时，$\dfrac mn+\dfrac nm$随着$\dfrac nm$的增大而减小，于是$\dfrac mn+\dfrac nm$的取值范围是$\left(2,\dfrac 52\right]$．
于是椭圆的离心率$e$的取值范围是$\left(\dfrac{\sqrt 2}2,\dfrac{\sqrt 5}3\right]$．
本题的关键是恰当地表达$Q$在椭圆上（绕开方程用定义）以及利用几何条件解三角形，同时对于多参数问题的化简与整理的方向也需要有一个明确的思路．
最后给出一道练习（2015高考数学重庆卷理科第21题），
如图，椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为$F_1$，$F_2$，过$F_2$的直线交椭圆于$P$，$Q$两点，且$PQ\perp PF_1$．若$|PF_1|=|PQ|$，求椭圆的离心率$e$．
答案 $\sqrt 6-\sqrt 3$．
提示 连接$QF_1$，并设$|PF_1|=m$，$|PF_2|=n$．
由$\triangle PF_1Q$是等腰直角三角形得$$|QF_2|=m-n,|QF_1|=\sqrt 2m.$$由椭圆的定义，有$$|PF_1|+|PF_2|=|QF_1|+|QF_2|,$$即$$m+n=\sqrt 2m+(m-n),$$从而$m=\sqrt 2n$．
因此椭圆的离心率$$e=\dfrac{2c}{2a}=\dfrac{|F_1F_2|}{|PF_1|+|PF_2|}=\dfrac{\sqrt{m^2+n^2}}{m+n}=\dfrac{\sqrt{\left(\sqrt 2n\right)^2+n^2}}{\sqrt 2n+n}=\sqrt 6-\sqrt 3.$$
更多相关问题见每日一题[329]定义 VS 方程．