若实数\(a,b\)满足\[\begin{cases}4^a+a=2\\{\log_2}\sqrt{2b+1}+b=2\end{cases}\]求\(a+b\)的值．
正确的答案是\(\dfrac 32\)．
法一 换元法
令\(t=a+b\)，则\(b=t-a\)，代入\[{\log_2}\sqrt{2b+1}+b=2\]中有\[{\log_2}\sqrt{2t-2a+1}+t-a=2,\]将对数式整理成指数式，有\[2t-2a+1=2^{4+2a-2t},\]将此式与已知条件的第一个式子在形式上尽量靠拢，有\[4^{a+\frac 32-t}+a=t+\frac 12,\]不难观察得\(t=\dfrac 32\)． 接下来补充证明\(t=\dfrac 32\)的唯一性． 事实上由已知条件的第一个式子可知\(a\)是唯一确定的（左边关于\(a\)是单调递增函数），用类似的方式可以说明\(t\)也是唯一确定的．
法二 数形结合
原方程组等价于\[\begin{cases}2^{2a+1}+(2a+1)=5\\{\log_2}\sqrt{2b+1}+b=2\end{cases}\]令\(u=2a+1\)，\(v=2b+1\)，则\[a+b=\frac 12(u+v)-1.\qquad\cdots (*)\]此时条件转化为\[\begin{cases}2^u+u=5\\{\log_2}v+v=5\end{cases}\]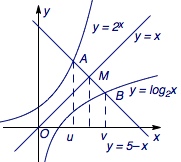 
于是\(u\)、\(v\)分别是函数\(y=2^x\)与函数\(y={\log_2}x\)的图象与直线\(y=5-x\)的交点横坐标，如图． 因为\(y=2^x\)与\(y={\log_2}x\)互为反函数，图象关于直线\(y=x\)对称，于是\[u+v=x_A+x_B=2x_M=5.\qquad\cdots (**)\] 由(*)(**)可得，\(a+b\)的值为\(\dfrac 32\)． 下面给出一道练习题（由刘艳辉提供）．
已知实数\(a>1\)，若函数\(y=a^{\frac x{\mathrm e}}\)的图象与函数\(y={\mathrm e}{\log_a}x\)的图象有两个不同的交点，则\(a\)的取值范围是_______． 答案是\((1,{\mathrm e})\)．