每日一题[297] 保值区间

这是我在QQ群中国数学解题研究会中看到的一个问题，由江苏无锡王举老师提供．

已知函数$f(x)=\left|x^2-a\right|$，其中$a>0$．若恰好有两组解$(m,n)$使得$f(x)$在定义域$[m,n]$上的值域也为$[m,n]$，求实数$a$的取值范围．

---

正确答案是$\left(\dfrac 34,2\right)$．

解    由于$f(x)\geqslant 0$，于是$m\geqslant 0\land m\neq \sqrt a$．按$\sqrt a$所在的位置分三种情况讨论．

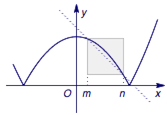
第一种情况，$m<n\leqslant \sqrt a$时．

此时$f(x)=-x^2+a$在$[m,n]$上单调递减，于是

$$\begin{cases} f(m)=n,\\f(n)=m, \end{cases}$$ 即 $$\begin{cases} -m^2+a=n,\\-n^2+2=m, \end{cases}$$ 两式相减得 $$m+n=1,$$ 于是$m$、$n$是关于$t$的方程 $$-t^2+a=1-t$$ 的两个根，如图1．

因此关于$t$的方程

$$t^2-t+1-a=0$$ 在$[0,\sqrt a]$有两个不等实根，即 $$\begin{cases} \left.\left(t^2-t+1-a\right)\right|_{t=0}\geqslant 0,\\\left.\left(t^2-t+1-a\right)\right|_{t=\sqrt a}\geqslant 0,\\0<\dfrac 12<\sqrt a,\\\Delta=1-4(1-a)>0,\end{cases}$$ 解得 $$\dfrac 34<a\leqslant 1.$$

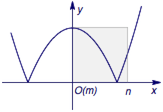
第二种情况，$m<\sqrt a<n$时．

此时必然有$m=0$，于是$f(x)$在区间$[m,n]$上的最大值为$f(0)$或$f(n)$．

如图2，若$n=f(0)$，则

$$n=a \land f(a)\leqslant a,$$ 解得 $$1<a \leqslant 2.$$

如图3，若$n=f(n)$，则

$$n=\dfrac{1+\sqrt{1+4a}}2\geqslant a,$$ 解得 $$a \leqslant 2.$$

而当$a=2$时以上两种情况对应的区间均为$[0,2]$．

第三种情况，$\sqrt a<m<n$时．

此时$f(x)$在定义域$[m,n]$上单调递增，于是

$$\begin{cases} f(m)=m,\\f(n)=n, \end{cases}$$ 也就是方程 $$f(x)-x=0$$ 在区间$(\sqrt a,+\infty )$上有两个不等实根．

但在区间$[m,n]$上，函数

$$h(x)=f(x)-x=x^2-x-a$$ 在$x=\sqrt a$处的函数值小于零，于是不能在区间$(\sqrt a,+\infty )$上有两个不同零点．

综合以上三种情况，$a$的取值范围是$\left(\dfrac 34,2\right)$．

当$a\in\left(\dfrac 34,1\right]$时，符合题意的两组解分别为

$$(m,n)=\left(\dfrac{1-\sqrt{4a-3}}2,\dfrac{1+\sqrt{4a-3}}2\right),\left(0,\dfrac{1+\sqrt{1+4a}}2\right);$$ 当$a\in(1,2)$时，符合题意的两组解分别为 $$(m,n)=(0,a),\left(0,\dfrac{1+\sqrt{1+4a}}2\right).$$